第三节 投资方案的类型与评价指标
一、投资方案的类型
投资方案的类型有三种:
(一)独立方案
所谓独立方案是指方案间互不干扰,即一个方案的执行不影响另一些方案的执行,在选择方案时可以任意组合,直到资源得到充分运用为止。
(二)互斥方案
所谓互斥方案,就是在若干个方案中,选择其中的任何一个方案,则其他方案就必然被排斥的一组方案。
(三)混合方案
在现实的经济生活中还存在着大量的在若干个互相独立的投资方案中,每个独立方案又存在着若干个互斥方案的问题,称它们之间的关系为混合方案。
二、不同类型投资方案的评价指标
(一)独立方案选择
1.独立方案的评价指标
在某种资源有限的条件下,从众多的互相独立的方案中选择几个方案时,采用的评价指标应该是“效率”,如果定性地表述“效率”指标,则可表述为:

这里的“制约资源”可以是资金,也可以是时间、空间、重量、面积等等,要依问题的内容而定。对于投资方案,这里所说的“效率”就是投资方案的内部收益率。
2.独立方案的选择方法
以教材中的X银行所面临的贷款问题为例说明独立方案选择的方法。为了简捷无误地解答上述X银行的问题,下面介绍一种应用“效率”指标进行独立方案选择的图解方法。该方法的具体步骤是:
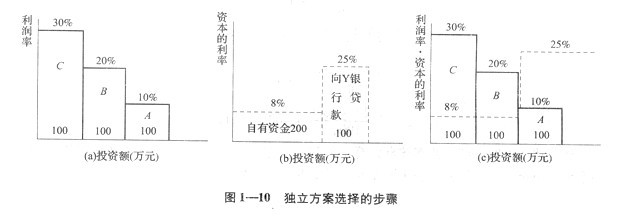
(1)计算各方案的“效率”,本题即为10%、20%、30%,也就是各方案的利率;将求得的数值按自大至小的顺序排列如图1-10(a)所示;
(2)将可以用于投资的资金成本,本题为8%和25%,由小至大排列如图1-10(b)所示;
(3)将上述两图合并成如图1-10(c)所示的形式;
(4)找出由左向右减少的“效率”线与由左向右增加的资金成本线的交点,该点左方所在的方案即是最后选择的方案。
由图1-10(c)可以看出:X银行最有利的选择应该是将自有资金200万元分别贷给C和B公司,由于Y银行利率为25%>10%,故不应向Y银行借款再转贷给A公司。
当我们熟悉了上述步骤之后,就无需画出图1-10中(a)、(b)、(c)三个图,只需画出(c)的形式即可进行独立方案的选择了。
3.独立方案选择的例题
[例1-6] 有8个互相独立的投资方案A、B、C、……H,投资的寿命期为1年,投资额及1年后的净收益如表1-2所示。当筹集资金的条件如下时,最优的选择是什么?
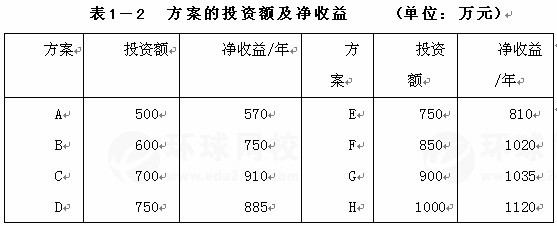
(1)资金筹集的数量没有限制,但资本的利率为下述三种情况:(a)i=10%;(b)i=13%;(c)i=16%。
(2)资本的利率为10%,但可利用的资金总额为3500万元。
(3)资金为1000万元时,利率为10%,此后每增加1000万元时,利率相应增加2%,最多可利用的资金总额为4000万元。
[解] 独立投资方案的选择指标是方案的内部收益率,为此,首先求出各方案的内部收益率。以A方案为例,采用净现值等于零的概念求解,则有:570×(P/F,r A,1)-500=0
(1)(a)i=10%时,只有E方案不合格,其他方案可全部采纳;
(b)i=13%时,E和H方案不合格,其他方案可全部采纳;
(c)i=16%时,A、E、C、H方案不合格,其他方案可全部采纳。
(2)按内部收益率的大小为序,依次选取C、B、F、D方案;此时总投资为2900万元,因资金限额为3500万元,所余资金600万元无法实施G方案;但因A方案投资为500万元,且其内部收益率14%>10%(资本利率),因而剩余资金可实施A方案。因而,此时最终选择的方案如下。应是:C、B、F、D、A。
(3)此时资本的利率如图中虚线所示,按内部收益率的大小为序依次选择。尽管资金的总额为4000万元,但是,除C、B、F、D方案之外,资本的利率皆大于方案的内部收益率;因此,最终选择的方案为:C、B、F、D。
例题1:某项目现有三个互斥的投资方案A、B、C,欲从中选择最有利的方案,一个投资方案的投资额及一年后的净收益如下表所示。各方案的寿命期都是一年,一年后的净残值为零。假设基准收益率为10%。
|
投资方案 |
投资额(万元) |
一年后的净收益(万元) |
|
A |
500 |
600 |
根据题意,回答下列问题:
(1)A方案的内部收益率为( )。
A.18%
B.20%
C.25%
D.27%
答案:B
解析:对于寿命期为1年的方案,其内部收益率=(净收益-投资额)÷投资额×100%,(600-500)÷500=20%。
(2)B方案的内部收益率为( )。
A.5%
B.8%
C.10%
D.20%
答案:C
解析:对于寿命期为1年的方案,其内部收益率=(净收益-投资额)÷投资额×100%,(660-600)÷600=10%。
(3)该项目方案的最佳选择为( )。
A.A方案
B.B、C两方案均可
C.C方案
D.A、B两方案均可
答案:A
解析:采用净现值法,A方案的净现值=-500+600÷(1+10%)=45.45(万元)。B方案的净现值=-600+660÷(1+10%)=0(万元)。C方案的净现值=-700+780÷(1+10%)=9.09(万元)。因此最佳选择为A方案。
例题2:现有A、B、C、D、E、F、C 7个互相独立的投资方案,各方案的投资额和1年后的净收益如下表所示。方案的寿命期都为一年,一年后的净残值为零,各个方案都是不可分割的(即不满足投资总额的要求,则该方案就不能成立)。若基准收益率为l0%,可利用的资金总额为1600万元时,其最佳的投资方案应是( )。

A.A、B、C、F
B.A、B、C、F、G
C.B、C、D、E、F
D.B、C、F、C
答案:A
解析:对于寿命期为1年的方案,其内部收益率=(净收益-投资额)÷投资额×100%,
rc=(540-400)÷400×100%=35%。
rB=(390-300)÷300×100%=30%。
rF=(870-700)÷700×100%=24%。
rD=(540-450)÷450×100%=20%。
rA=(230-200)÷200×100%=15%。
rG=(900-800)÷800×100%=13%。
rE=(550-500)÷500×100%=10%。
C、B、F、D内部收益率最大,都大于基准收益率为l0%,但是可利用的资金总额为1600万元,因此,最佳的投资方案应是C、B、F、A。
4.内部收益率指标的适用范围
(1)各投资方案净收益类型不同的情况
对于投资类型截然不同的方案,在进行方案选择时不宜采用内部收益率作为评价的指标使用,而宜采用现值法(年值法、将来值法)。
(2)有多个内部收益率的情况
求内部收益率实际是求方程的根,对于n次方程就可能存在着n个实数根,因而就对应着n个内部收益率。此时用内部收益率判定该方案是否可行是困难的。
★★★在进行方案选择时,只要注意以下几点就可以避免判断上的错误:
①对于初期投资之后有连续的正的净收益的方案,没有两个以上实数根(即内部收益率);
②具有多个内部收益率的投资方案是各期净现金流量有时为正有时为负的情况,此时不宜采用内部收益率作为判断方案优劣的依据;
③通常具有多个内部收益率的投资方案往往其净现值很小,因而研究方案时将这些方案排除在外通常不会有大的差错;
④对于(1)中所讲的那种投资类型完全不同的情况,不宜采用内部收益率作为判断的指标。
例题1:下列类型的投资方案中,适于使用内部收益率法进行评价的是( )。(2009年试题)
A.独立方案
B.寿命期不同的互斥方案
C.寿命期相同的互斥方案
D.混合方案
答案:A
解析:此题考核的是独立方案的评价指标、评价方法。对于投资类型截然不同的方案,在进行方案选择时不宜采用内部收益率作为评价的指标使用,而宜采用现值法(年值法、将来值法)。在比较寿命期不同的互斥方案时常常使用年值法。互斥方案的选择标准有很多,例如净现值、净年值、净将来值法,差额的净现值、净年值、净将来值法,追加投资收益率法等。
例题2:下列投资方案评价方法中,不可以用独立方案选择的有( )。(2007年试题)
A.投资回收期法
B.内部收益率法
C.差额法
D.净现值法
E.最小公倍数法
答案:CE
解析:独立方案选择可用内部收益率法、投资回收期法、净现值法。
(二)互斥方案选择
1.净现值、净年值、净将来值法
对于单一的投资方案,当给定基准收益率或设定的收益率后,只要求得的净现值、净年值或净将来值大于等于零,那么该方案就可以考虑接受。
(1) 净现值法
净现值法就是将包括初期投资额在内的各期的现金流量折算成现值再比较的方法。主要利用等额支付现值因数(P /A,i,n)。
例题:某方案现时点投资23万元,此后从第2年年末开始,连续20年,每年将有6.5万元的净收益,净残值为6.5万元。若基准收益率为20%,己知: (P/A,20%,20)=4.8696,(P/F,20%,21)=0.0217,则该方案的净现值是( )万元。(2009年试题)
A.2.57
B.3.23
C.3.52
D.4.35
答案:C
解析:此题考核的是净现值的求法。用(P/A,20%,20)求出净收益的现值=6.5×4.8696/(1+20%)=26. 377万元;用(P/F,20%,21)求出净残值的现值=6.5×0.0217=0. 1411万元;则该方案的净现值=-23+26.377+0. 1411=3.5181万元。
(2)净将来值法
用净将来值法比较方案优劣时,只要将每年的净收益值与等额支付将来值因数(F/A,i,n)相乘,初期投资额与一次支付复本利和因数相乘,两者相减即可。
例题:现在投资10万元购买某设备,则今后6年内每年年末将花5万元的维护费用,而在第3年和第5年年初还将花费8万元的修理费用。若资本利率i=10%,则6年年末为止支付的总费用的复本利和为( )万元。已知:(F/P,10%,6)=1.772,(F/P,10%,4)=1.464,(F/P,10%,2)=1.210,(F/A,10%,6)=7.716。
A.86.486
B.83.284
C.79.860
D.77.692
答案:D
解析:FW=10×1.772+5×7.716+8×1.464+8×1.210=77.692万元。
(3)净年值法
只要将初期投资额乘以资本回收因数(A /P,i,n),将其折算成年值即可。
例题1:某商店正在研究购买经营用的冷藏设备哪个更有利的问题。S装置的价格为5万元,寿命为5年;与此性能完全相同的Q装置的寿命为8年,该商店的基准收益率为12%,则Q装置的价格为( )万元以下时比S装置有利。已知:(A/P,12%,5)=0.27741,(A/P,12%,8)=0.20130。
A.8.24
B.6.89
C.7.46
D.8.86
答案:B
解析: 这是寿命期不同的互斥方案选择的问题,宜采用净年值法。设Q装置的价格为P,则Q设备较S设备有利的条件是:
5× (A/P,12%,5)≥P (A/P,12%,8)。
故有:P≤5× (A/P,12%,5)÷(A/P,12%,8)= 5×0.27741÷0.20130=6.89万元。
例题2:某投资方案初期投资额为300万元,此后每年年末的作业费用为40万元。方案的寿命期为10年,10年后的净残值为零。若基准收益率i= 10%,则该方案投资及总作业费用的年值为( )万元。已知:(A/P,10%,10)=0.16275。
A.79.45
B.76.46
C.80.86
D. 88.83
答案:D
解析:PW=-300-40/(A/P,10%,10)=-300-40/0.16275=545.77573;
AW=545.77573×(A/P,10%,10)=545.77573×0.16275=88.83万元。
2.差额法
★★★差额法内涵:研究两方案现金流量的差额,由差额的净现值、净年值和净将来值的正负判定方案的优劣是有效的方法,这种方法就是差额法。
差额法包括差额的净现值法、差额的净年值法和差额的净将来值法。
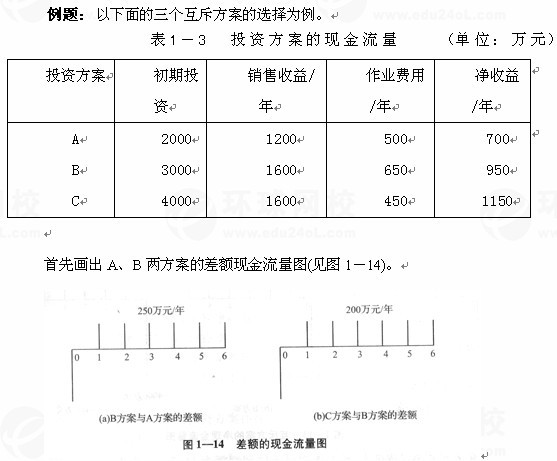
(1)利用差额的净现值法计算和判别
B方案较A方案初期投资多1000万元,每年的净收益多250万元。用PW(B-A)表示B方案较A方案增加的现金流量的净现值,则有:
PW(B-A)=PWB-PW A=(950-700)×(P/A,10%,6)-(3000-2000)=250×(P/A,10%,6)-1000=88(万元)>0
★★★PW(B-A)>0,说明B方案的净现值较A方案的净现值大,因而可以判断B方案较A方案有利。
同样,图1-14(b)表示的是C方案较B方案增加值的差额现金流量图,其差额的现值为:
PW(C-B)=PWC-PWB=200×(P/A,10%,6)-1000=-129(万元)<0
(2)用差额的净年值法判定时,则有:
AW(B-A)=250-1000×(A/P,10%,6)=20(万元)>0
(3)用差额的净将来值法判定时,则有:
FW(B-A)=250×(F/A,10%,6)-1000×(F/P+10%,6)=157(万元)>0
★★★用“差额的净现值法”、差额的净年值法”、“差额的净将来值法” 来计算和判别,其结论都是相同的。
例题:现有两个可供选择的设备购置方案A和B:A方案的初期投资为2万元,寿命期为10年,年运行费用为l万元;B方案的初期投资额为1.7万元,寿命期也为10年,年运行费用为1.3万元。i=8%,则A方案较B方案相当于现时点少投入( )元。已知:(P/A,8%,10)=6.710。
A.17650 B.16456 C.18747 D. 17130
答案:D
解析:PWA=-2-1(P/A,8%,10)=-2-1×6.710=-8.71万元。
PWB=-1.7-1.3(P/A,8%,10)=-1.7-1.3×6.710=-10.423万元。
PWA-PWB =-8.71-(-10.423)=1.713万元。
3.追加投资收益率法
追加投资收益率就是追加投资(投资的增加额)的收益比率。追加投资收益率(亦称差额投资收益率)是进行互斥方案选择时的重要评价指标。
值得注意的是:当我们将各方案联结成单调减少的折线形式之后,发现B、D两方案在该折线之下,我们称这种方案为无资格方案。所谓无资格方案就是在互斥方案选择时,该方案不可能成为最终选择的方案(其证明从略),因而在方案选择之前将其排除在外,将使方案的选择简化。
由于本题中B、D方案是无资格方案,将其排除后就意味着:C方案是在A方案的基础上追加投资400-200=200(万元)而成;E方案是在C方案的基础上追加投资600-400二200(万元)而成;此时需计算该追加投资额的收益能力--追加投资收益率,其计算过程如下:
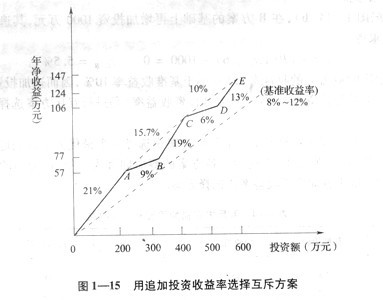
若联结成的折线是单调减少的形式,则无需进行排除无资格方案的过程,直接进行方案选择即可。
例题:下列评价方法中,可用于寿命期相同的互斥方案选择的有( )。(2009年试题)
A.净现值法
B.内部收益率法
C.净年值法
D.最小公倍数法
E.追加投资收益率法
答案:ACE
解析:此题考核的是寿命期相同的互斥方案选择的方法。互斥方案的选择标准有很多,例如净现值、净年值、净将来值法,差额的净现值、净年值、净将来值法,追加投资收益率法等。在比较寿命期不同的互斥方案时常常使用年值法、最小公倍数法。
4.寿命期不同的互斥方案选择
上面讲述的互斥方案选择都是假定各方案的投资寿命期(服务年限)完全相同的情况下进行的。但是,现实中很多方案的寿命期往往是不同的。
比较寿命期不同方案的优劣时,严格地说,应该考虑至各投资方案寿命期最小公倍数为止的实际可能发生的现金流量。在比较寿命期不同的互斥方案时常常使用年值法。
注:最小公倍数对于两个整数来说,指该两数共有倍数中最小的一个。计算最小公倍数时,通常会借助最大公约数来辅助计算。
当我们遇到寿命期不同的互斥方案选择时,应首选净年值法。
例题1:在下述方法中,最适合作为寿命期不同的互斥方案选择的方法是( )。(2006年试题)
A.净现值法
B.差额法
C.净年值法
D.净将来值法
答案:C
解析:寿命期不同的互斥方案选择看,严格地说,应该考虑至各投资方案寿命期最小公倍数为止的实际可能发生的现金流量。但是,预测遥远未来的实际现金流量往往是相当困难的。为了简化计算,通常总是假定第一个寿命期以后的各周期所发生的现金流量与第二个周期的现金流量完全相同地周而复始地循环着,然后求其近似解,进行方案的比较与选择。在比较这类寿命期各异的投资方案时,年值法要比现值法和将来值法方便得多,因此,在比较寿命期不同的互斥方案时常常使用年值法。
例题2:下列各类投资方案中,适合使用差额法进行选择的是( )。(2008年试题)
A.寿命期相同的互斥方案
B.寿命期不同的互斥方案
C.独立力案
D.混合方案
答案:A
解析:此题主要是考查互斥方案的选择,当我们遇到寿命期不同的互斥方案选择时,应首选净年值法。
例题3:下列方案中,适于采用最小公倍数法进行方案评价的是( )。(2008年试题)
A.独立方案
B.寿命期不同的互斥方案
C.单一投资方案
D.混合方案
答案:B
解析:此题主要是考查互斥方案的选择,适用最小公倍数法的是寿命期不同的互斥方案。
例题4:以下各指标中,可以作为寿命期不同的投资方案选择的是( )。(2005年试题)
A.差额的净现值
B.净年值
C.追加投资收益率
D.内部收益率
答案:B
解析:当我们遇到寿命期不同的互斥方案选择时,应首选净年值法。
(三)应用投资回收期时应注意的问题
回收期的长短对评价方案优劣是不起作用的。回收期仅仅是一个表明投资得到补偿的速度指标,是个时间的限值。长远看回收期是不能解决根本问题的。
因此,回收期法不宜作为一个指标单独使用,只能作为辅助性的参考指标加以应用。
注:静态投资回收期和动态投资回收期二者产生差距的原因:在于动态投资回收期考虑了资金的时间价值,而静态投资回收期没有考虑资金的时间价值。
一、静态投资回收期是在不考虑资金时间价值的条件下,以项目的净收益回收其全部投资所需要的时间。投资回收期可以自项目建设开始年算起,也可以自项目投产年开始算起,但应予注明。其计算公式:
P t =累计净现金流量开始出现正值的年份数-1+上一年累计净现金流量的绝对值/出现正值年份的净现金流量
二、动态投资回收期是把投资项目各年的净现金流量按基准收益率折成现值之后,再来推算投资回收期,这就是它与静态投资回收期的根本区别。动态投资回收期就是净现金流量累计现值等于零时的年份。其计算公式:
P't =(累计净现金流量现值出现正值的年数-1)+上一年累计净现金流量现值的绝对值/出现正值年份净现金流量的现值
附第一章课后部分习题解析:
一、单项选择题
1.如现在投资10万元,预计年利率为10%,分5年等额回收,每年可回收( )万元。已知:(A/P,10%,5)=0.26380。
A.2.638
B.2.138
C.2.100
D.2.771
答案:A
2.某建筑企业向金融机构贷款500万元,按复利计息,年利率i=12%。若第五年末一次还本付息,应偿还( )万元。已知:(F/P,12%,5)=1.762。
A.881.00
B.801.17
C.811.71
D.818.17
答案:A
解析:F=P(F/P,12%,5)=500×1.762=881万元。
3.某人现年40岁,现有2万元存款,因为他将在60岁时退休,退休时他想有10万元存款,以保证生活水平不至降低。假设退休时单位可以支付1万元退休金,从现在开始每年年末他将均等地存入银行一笔钱,那么,为达到退休时有10万元的积蓄,则应存款( )元。已知:(F/P,5%,20)=2.653,(F/A,5%,20)=33.066。
A.2456.4
B.1117.2
C.3256.7
D.1846.7
答案:B
解析:由(F/A,5%,20)=33.0660导出,(A/F,5%,20)=0.003。
A=[10-2×(F/P,5%,20)-1] ×(A/F,5%,20)= 0.1117(万元)。
4.某债券现在购买需花10万元,6年后可得20万元,若将购买债券看做是按复利向银行存款,那么相当于银行存款的利率是( )。
A.10.645%
B.11.476%
C.13.456%
D.12.241%
答案:D
解析:根据题意有:F=P(F/P,i,n),即:20=10(F/P,i,6) 所以 (F/P,i,6)=2。
由于:(F/P,12%,6)=1.974,(F/P,13%,6)=2.082。可知相当于银行存款的利率在12%~13%之间,用插值法可得利率。
5.年利率为6%,设每季度复利一次,若10年内每季度都能得到500元,则现在应存款( )元。
A.12786
B.15697
C.14958
D.13469
答案:C
6.某人现在存款1000元,单利年利率为2.25%,则5年年末本利和为( )元。
A.1191
B.1113
C.1146
D.1025
答案:B
解析:如果用P表示本金的数额,n表示计息的周期数,i表示单利的利率,I表示利息数额,则其利息I=P·n·i=1000×5×2.25%=112.50(元) ;则5年年末本利和=1000+112.50=1112.50元。
7.某人从现在开始每年年末均等地存入银行1000元,年利率为6%,则4年末复本利和应为( )元。
A.4672
B.4375
C.4782
D.4267
答案:B
8.某投资项目,现时点投资1000万元,则自第一年年末开始,每年年末都将有均等的净收益240万元,若i=5%,经营期可以看做是无限,则该项目相当于现时点的净收益为( )万元。
A.5600
B.4950
C.3800
D.4200
答案:C
解析:此题主要是考查的是永续年值(n趋于无穷大)的情况,P=A/i。P=240÷5%-1000=3800(万元)。
9.某设备的购置费用为50万元,基准收益率为10%,欲在10年内将该投资的复本利和全部回收完了,则每年均等的折旧费应计提( )万元。已知:(A/P,10%,10)=0.16275。
A.9.452
B,8.138
C.7.546
D.9.825
答案:B
解析:A=P(A/P,10%,10)=50×0.16275=8.1375万元。
10.某自动化设备投资24万元之后,每年可以节约人工费用6万元(假设发生于每年年末),那么,该设备的寿命期为( )年时,该项投资是合适的。设i=12%。
A.4.56
B.6.78
C.5.78
D.5.25
答案:C
解析:PW=-24+6(P/A,12%,n)≥0;(P/A,12%,n)≥4,而(P/A,12%,5)=3.6048;(P/A,12%,6)=4.1114。n≥5+(4-3.6048)/(4.1114-3.6048)=5.78。
11.某城市环保部门准备在临江的污水排水口处建立污水处理装置。采用该装置,现时点的投资为2000万元,此后每隔4年就需要500万元的维修清理费用。该装置的寿命期可以认为是无限的。若资本的利率为12%,则整个运行期间的全部费用额的现值应为( )万元。已知:(A/F,12%,4)=0.20923。
A.3484
B.2642
C.2872
D.2986
答案:C
解析:A=F(A/F,12%,4)=500×0.20923=104.615万元。
P=A/12%+2000=104.615/12%+2000=2872万元。
12.某人在孩子5岁时将一笔资金存入银行,假设银行的年利率为5%,按复利计息,若想满足孩子在18岁和24岁时都能取出2万元,则该人现在应存( )万元。已知:(P/F,5%,13)=0.5303,(P/F,5%,19)=0.3957。
A.1.646
B.3.240
C.2.455
D.1.852
答案:D
解析:2×0.3957+2×0.5303=1.852万元。
13.某地区拟建收费的高速公路,所需资金:现时点为4亿元,此后第1、2、3年年末各需2亿元(3年内合计投资10亿元),修成后每隔5年维修一次,每次修理费用1000万元。若基准收益率为8%,则该道路自开通(3年后)起维持40年所需总投资额(包括初期投资和维修费在内)的现值为( )亿元。已知:(P/A,8%,3)=2.577,(A/F,8%,5)=0.17046,(P/A,8%,40)=11.925,(P/F,8%,3)=0.7938。
A.12.426
B.10.325
C.9.315
D.11.428
答案:C
解析:此题有问题,解题思路应是:4+2×2.577+0.1÷(A/F,8%,5) ÷(F/A,8%,40)÷(P/F,8%,3)。但(F/A,8%,40)未给出。
相关推荐:- 培训课程
- 更多课程报名入口>>
在线课程 |
2024年
学考双赢定制班 63%学员选择 |
2024年
学考双赢黑卡班 31%学员选择 |
2024年
学考双赢取证班 6%学员选择 |
2024年
专项提分班 |
||
| 学 | 基础学习 拿分阶段 |
私教精讲班 | ||||
| 强化学习 提分阶段 |
重要考点提炼班 | |||||
| 练 | 冲刺密训 抢分阶段 |
8套名师密押卷 | ||||
| 背 | 考前终极 抢分阶段 |
通关必备200题 | ||||
| 考前3小时密训班 | ||||||
| 专项班 | 经济基础: 图形/计算题专项 |
|||||
| 专业课: 案例专项专项 |
||||||
| ★★★ 三星题库 ¥680/年 |
每日一练 |
|||||
每日错题榜 |
||||||
章节刷题 |
||||||
| ★★★★ 四星题库 ¥980/年 |
真题题库 |
|||||
高频常考 |
||||||
大数据易错 |
||||||
| ★★★★★ 五星题库 ¥1680/年 |
通关必备200题 |
|||||
名师密押8套卷 |
||||||
| 教学资料 | 课程讲义 | |||||
| 全程学习计划书 | ||||||
| 人工助学服务 | 微信一对一 班主任督学 7×13陪伴模式 |
|||||
| 老师微信 一对一答疑 |
||||||
| 定制服务 无忧从容包 |
无忧从容卡 ¥980 | |||||
| 专项突破班 ¥1360 | ||||||
| 黑卡特权 | 不过退费 | |||||
| 额外赠送 | 赠送2023年 【教材精讲班】 |
赠送2023年 【教材精讲班】 |
赠送2023年 【教材精讲班】 |
|||
| 课程有效期 | 2024年11月30日 | 2025年11月30日 | 2024年11月30日 | 2024年11月30日 | ||
| 套餐价格 | 全科:¥4680 单科:¥2880 |
全科:¥9880 单科:¥5980 |
全科:¥1580 单科:¥880 |
全科:¥1080 单科:¥680 |
||
·2020中级经济师考试《金融专业》考前背诵考点 (2020-11-19 11:52:45)
·2020中级经济师《人力资源》考前背诵考点 (2020-11-19 11:47:40)
·2020年中级经济师考试《财政税收》税率汇总 (2020-11-19 11:43:09)
·《人力资源管理》关于时间和数字的考点汇总 (2020-11-16 7:31:38)
·《人力资源管理》关于时间和数字的考点(3) (2020-11-16 11:29:53)
·免费真题 ·模考试题


实用文档 | 入党资料 | 入党申请书 | 入党志愿书 | 个人自传 | 转正申请书 | 思想汇报 | 个人简历 | 简历模板 | 简历封面 | 工作计划 | 工作总结 | 自我评测
个性评测 | 社交评测 | 事业评测 | 运势评测 | 报告 | 实习报告 | 工作总结 | 社会实践 | 心得体会 | 述职报告 | 调查报告 | 辞职报告
法律文书 | 合同范本 | 演讲范文 | 更多>>
英语学习 | 听力口语 | 阅读写作 | 翻译文化 | 趣味英语 | 学习方法 | 英文经典歌曲 | 每日课堂 | 空中英语 | 少儿英语 | 影视英语 | 英文歌曲 | 更多>>
作文大全 | 作文 | 小学 | 初中 | 高中 | 话题作文 | 考研 | 四六级 趣味作文 | 体裁作文 | 记叙文 | 议论文 说明文 | 应用文 | 读后感 | 作文素材 | 名言警句
优美段落 | 哲理故事 | 诗词赏析 | 成语知识 | 技巧 | 写作指导 | 作文点评 | 佳文赏析 | 写作基础 | 话题演练 | 作文教学 | 更多>>


 下载
下载



































