| 第 1 页:二、比率法 |
| 第 2 页:三、期间法 |
第二节 单一投资方案的评价
【考试目的】
测查应试人员是否掌握资金时间价值计算的有关概念,并能应用资金时间价值计算公式解决具体问题;
【考试内容】
净现值、净年值、净将来值、基准收益率、内部收益率、投资回收期的基本概念,并应用上述概念熟练地进行单一方案的评价。
【本节主要内容】
1.数额法-净现值
2.比率法-内部收益率
3.期间法-投资回收期
一、数额法
数额法也称为绝对量值法。
(一)基准收益率
基准收益率
◇所谓基准收益率,就是企业或者部门所确定的投资项目应该达到的收益率标准。
◇是投资决策的重要参数,部门和行业不同,其值通常是不同的,当价格真正反映价值时该值才趋于相同。
◇通常该值不能定得太高或太低:太高,则可能使某些投资经济效益好的被淘汰;太低,则可能使某些投资经济效益差的被采纳。基准收益率一般大于贷款利率。
【例1·单选题】基准收益率与贷款的利率是不同的,通常基准收益率应 ( )贷款的利率。
A.小于
B.大于
C.等于
D.等于或小于
『正确答案』B
『答案解析』基准收益率与贷款的利率是不同的,通常基准收益率应大于贷款的利率。
(二)净现值、净年值、净将来值
净现值(NPV或PW)是投资方案在执行过程中和生产服务年限内各年的净现金流量(现金流入减现金流出的差额)按基准收益率或设定的收益率换算成现值的总和。
净年值(AW)通常又称为年值,是将投资方案执行过程中和生产服务年限内的净现金流量利用基准收益率或设定的收益率换算成均匀的等额年值。
净将来值(FW)通常称为将来值,是将投资方案执行过程中和生产服务年限内的净现金流量利用基准收益率或设定的收益率换算成未来某一时点(通常为生产或服务年限末)的将来值的总和。
【注意】
■ 净现值、净年值、净将来值三者一般不相等
■ 三者中要有一个为零则全为零
※本部分考试采分点:净现值、净年值、净将来值概念及特点。
【例2·单选题】某投资方案初期投资额为2000万元,此后从第二年年末开始每年有净收益,方案的运营为10年,寿命期结束时的净残值为零。若基准收益为12%,则该投资方案的年净收益为( )万元时,该投资方案净现值为零。已知:(P/A,12%,10)=5.650;(P/F,12%,1)=0.8929。(2006年试题)
A.362
B.378
C.386
D.396
『正确答案』D
『答案解析』-2000+A×5.650×0.8929=0。A=396(万元)。
(三)数额法
数额法的实质就是根据基准收益率或设定的收益率,将投资方案的净现金流量换算成净现值或净年值、净将来值,然后按上述值是大于、等于或小于零来判断方案是可以接受,还是不可以接受的方法。
通常的投资方案是在初期有一笔投资额C0,此后第1、2、…n期末有R1、R2…Rn。净收益的情况(见图1-8)。根据资金时间价值的计算公式即可得到净现值、净年值和净将来值。
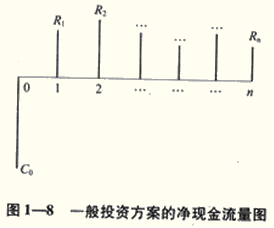
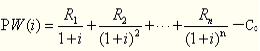
上式即为净现值(PW):
①当该值为零时,表明该投资方案恰好满足给定的收益率;
②若该值为正值,说明该方案除能保证给定的收益率之外,尚较通常的资金运用机会获得的收益要大;
③该值若为负值,则说明该方案不能满足预定的收益率或其收益小于通常资金运用机会的收益。因此,当该值≥0时,该投资方案可以接受,否则不宜接受。
求出净现值之后,只要应用已知现值求年值的公式即可求得净年值:
净年值AW(i)=PW(i)(A/P,i,n)
同样,可求出净将来值(FW)如下:
净将来值FW(i)=PW(i)(F/P,i,n)
或者 净将来值FW(i)=R1(1+i)n-1+R2(1+i)n-2+…+Rn-Co(1+i)n (1-9)
净现值、净年值和净将来值是投资方案是否可以接受的重要判断依据之一,它们反映了方案较通常投资机会收益值增加的数额,尤其是净现值更能给出这种收益增加值的直观规模。但进行这种计算时须事先给出基准收益率或设定收益率。值得说明的是:在应用这三个指标时,哪个方便即可应用哪个,其结论是相同的。
※本部分考试采分点:净现值、净年值、净将来值的判别原则。
【例3·单选题】某永久性投资项目投资初始额为30万元,从第一年起,每年年末可产生净收益5万元,假设基准收益率为10%,则项目的净现值为( )万元。(2010年真题)
A.-5
B.5
C.10
D.20
『正确答案』D
『答案解析』本题考查净现值的计算。已知现值P=30万元,期限为无限年,基准收益率i=10%。
年值A=5万元。净现值=A/i-30=5/10%-30=20万元。
【例4·单选题】某债券现在购买需12万元,6年后出售可得32万元,基准收益率为8%,则该项投资收益的净现值是( )万元。已知:(P/F,8%,6)=0.6302。(2010年真题)
A.8.166
B.9.260
C.10.285
D.11.456
『正确答案』A
『答案解析』本题考查净现值的计算。已知现值P=12万元,期限n=6年,终值F=32万元,基准收益率i=8%。净现值=F×(P/F,8%,6)-P=32×0.6302-12=8.166万元。
【例5·单选题】某方案现时点投资23万元,此后从第2年年末开始,连续20年,每年将有6.5万元的净收益,净残值为6.5万元。若基准收益率为20%,己知:(P/A,20%,20)=4.8696,(P/F,20%,21)=0.0217,则该方案的净现值是( )万元。 (2009年真题)
A.2.57
B.3.23
C.3.52
D.4.35
『正确答案』C
『答案解析』本题考核的是净现值的求法。
把每年净收益折为第2年初现值P1=A(P/A,20%,20)=6.5×4.8696=31.6524
把每年净收益折为现值(0点位置)P2=P1/(1+r)=31.6524/120%=26.377
把净残值折为现值P3=F(P/F,20%,21)=6.5×0.0217=0.14105
所以,净现值=26.377+0.14105-23=3.52
NPV=6.5(P/A,20%,20)(P/F,20%,1)+6.5(P/F,20%,21)-23=3.52
本题易错处
■ 忘记最后减去初始投资23万元
■ 忘记残值也需要折现
■ 将20年收益折现时,忘记只折在第1年年末,还需要再折算一次,折到0点位置
二、比率法
比率法与数额法都是经常使用的,但二者有很大的区别。前者是相对数,后者是绝对数。比率有很多种,其中被广泛采用的是内部收益率。
关于内部收益率的概念、求法和应用。
(一)内部收益率的概念
用一个具体的例子说明内部收益率的概念。
投资1000万元购置某固定资产后,第一年、第二年、第三年年末分别可获得600万元、500万元、400万元净收益,其寿命为3年,3年后的净残值为零。假如将该投资问题加以抽象,看做是向银行存款,则银行存款的利率r (该值即为内部收益率)应该是多少?
第一年年末:1000×(1+r)-600
第二年年末:[1000×(1+r)-600]×(1+r)-500
第三年年未:{[1000×(1+r)-600]×(1+r)-500}×(1+r)-400
因第三年年末的存款余额为零,故有下式成立:
1000×(1+r)3-600×(1+r)2-500×(1+r)-400=0
即:600×(1+r) 2+500×(1+r)+400-1000×(1+r) 3=0 (1-10)
上式左边恰是该方案现金流量的净将来值。因此,由上式可以得到:所谓内部收益率,就是使方案寿命期内现金流量的净将来值等于零时的利率。
如果用(1+r) 3去除(1-10)式的两边,则有:
(1-11)式左边恰是该方案现金流量的净现值。因此,可以说,所谓内部收益率,是指方案寿命期内使现金流量的净现值等于零时的利率。
同理,可以定义为:使现金流量的净年值为零时的利率即是该方案的内部收益率。
事实上,根据净现值、净年值、净将来值的相互换算公式可知,只要三者之中的任何一个为零,其他两个肯定为零。因而,采用任何一种形式定义内部收益率,其结果都是相同的。
※本部分考试采分点:内部收益率概念及特点。
(二)内部收益率的求法
■ 内部收益率函数是减函数
◇ i1时,净现值为PW1>0,则r一定比i1大
◇ i2时,净现值为PW2<0,则r一定比i2小
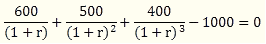

先假定一个r值,当两次假定的r值使净现值由正变为负,或者由负变为正时,根据数学的概念可知,在两者之间必定存在使净现值等于零的r值,该值即为欲求的该方案的内部收益率。具体求解时可采用插值法。
■ 计算方法-插值法
◇ i1时,净现值为NPV1>0
◇ i2时,净现值为NPV2<0
【例6·单选题】某建设项目,当i1=12%时,净现值为860万元,当i2=18%时,净现值为-600,基准收益率为10%,则该项目的内部收益率应( )。
A.在12%和10%之间
B.小于12%
C.在12%和18%之间
D.大于18%
『正确答案』C
『答案解析』内部收益率一定夹在哪个值中间。
【例7·单选题】某项目贷款100万元,要求在3年内每年年末等额偿还40万元,则该笔贷款的利率是( )。已知:(P/A,8%,3)=2.5770,(P/A,10%,3)=2.4870。(2010年真题)
A.8.56%
B.8.69%
C.9.54%
D.9.71%
『正确答案』D
『答案解析』本题考查插值法计算。已知现值P=100万元,期限n=3年,年值A=40万元。
因为题干给出了(P/A,8%,3)=2.5770,(P/A,10%,3)=2.4870,所以可以采取试算法,当i1=8%时,净现值PW1=40×(P/A,8%,3)-100=3.08万元;当i2=10%时,净现值PW2=40×(P/A,10%,3)-100=-0.52万元。
所以,可以进一步采取插值法计算,假设贷款利率为i,i1=8%,i2=10%, i1 i= i1+(i2- i1)×PW1/(|PW1|+|PW2|) =8%+(10%- 8%)×3.08/(|3.08|+|-0.52|) =9.71% 。 【例8·单选题】某建设项目,当资本利率il=12%时,净现值为860万元;当i2=18%时,其净现值为-540万元,则该建设项目的内部收益率是( )。(2008年真题) A.8.31% B.14.31% C.15.69% D.21.69% 『正确答案』C 『答案解析』假设i1 内部收益率(IRR)=12%+(18%-12%)×860/(860+540)=15.69%。 还可以排除法,内部收益率一定在12%和18%之间,AD首先就被排除了。 (三)内部收益率与方案评价 ■ 实质 ◇ 利用内部收益率指标来评价项目 ◇ 评价项目本身的考虑了资金时间价值的收益能力(对应的静态指标是投资利润率) ■ 判定标准 ◇ 内部收益率大于或等于基准收益率或设定的收益率,表明项目可接受 ◇ 内部收益率小于基准收益率或设定的收益率,则方案不可接受 ■ 说明 ◇只要内部收益率大于基准收益率,净现值就一定大于0,反之亦然 ◇无论采用数额法还是比率法,其结论都是相同的,由其中的任何一种结论都可以推导出另外一种相同的结论。 ※本部分考试采分点:内部收益率的判别原则。 【例9·多选题】某建设项目,当i1=12%时,净现值为450万元;当i2=15%时,净现值为-200万元,平均资金成本率为13.2%,基准收益率为l0%,则该项目( )。(2009年真题) A.内部收益率在l2~15%之间 B.净现值小于零 C.可行 D.净年值小于零 E.净将来值小于零 『正确答案』AC 『答案解析』本题考核的是单一投资方案的评价方法。A.净现值为零时的收益率即为该方案的内部收益率,所以内部收益率在l2~15%之间是正确的;C该项目的内部收益率大于基准利率,所以该项目可行,只要内部收益率大于基准收益率,净现值就一定大于零,净年值、净将来值也都大于零所以BDE不正确。 【例10·多选题】下述关于内部收益率的说法中,正确的是( )。(2006年真题) A.内部收益率是使方案净现值等于零时的折现率 B.内部收益率大于等于基准收益率时,方案可行 C.内部收益率小于等于基准收益率时,方案可行 D.插值法求得的内部收益率大于方案真实的内部收益率 E.插值法求得的内部收益率小于方案真实的内部收益率 『正确答案』ABD 『答案解析』内部收益率大于等于基准收益率时,方案可行。插值法求得的内部收益率大于方案真实的内部收益率。 相关推荐:
- 培训课程
- 更多课程报名入口>>
在线课程 |
2024年
学考双赢定制班 63%学员选择 |
2024年
学考双赢黑卡班 31%学员选择 |
2024年
学考双赢取证班 6%学员选择 |
2024年
专项提分班 |
||
| 学 | 基础学习 拿分阶段 |
私教精讲班 | ||||
| 强化学习 提分阶段 |
重要考点提炼班 | |||||
| 练 | 冲刺密训 抢分阶段 |
8套名师密押卷 | ||||
| 背 | 考前终极 抢分阶段 |
通关必备200题 | ||||
| 考前3小时密训班 | ||||||
| 专项班 | 经济基础: 图形/计算题专项 |
|||||
| 专业课: 案例专项专项 |
||||||
| ★★★ 三星题库 ¥680/年 |
每日一练 |
|||||
每日错题榜 |
||||||
章节刷题 |
||||||
| ★★★★ 四星题库 ¥980/年 |
真题题库 |
|||||
高频常考 |
||||||
大数据易错 |
||||||
| ★★★★★ 五星题库 ¥1680/年 |
通关必备200题 |
|||||
名师密押8套卷 |
||||||
| 教学资料 | 课程讲义 | |||||
| 全程学习计划书 | ||||||
| 人工助学服务 | 微信一对一 班主任督学 7×13陪伴模式 |
|||||
| 老师微信 一对一答疑 |
||||||
| 定制服务 无忧从容包 |
无忧从容卡 ¥980 | |||||
| 专项突破班 ¥1360 | ||||||
| 黑卡特权 | 不过退费 | |||||
| 额外赠送 | 赠送2023年 【教材精讲班】 |
赠送2023年 【教材精讲班】 |
赠送2023年 【教材精讲班】 |
|||
| 课程有效期 | 2024年11月30日 | 2025年11月30日 | 2024年11月30日 | 2024年11月30日 | ||
| 套餐价格 | 全科:¥4680 单科:¥2880 |
全科:¥9880 单科:¥5980 |
全科:¥1580 单科:¥880 |
全科:¥1080 单科:¥680 |
||
·2020中级经济师考试《金融专业》考前背诵考点 (2020-11-19 11:52:45)
·2020中级经济师《人力资源》考前背诵考点 (2020-11-19 11:47:40)
·2020年中级经济师考试《财政税收》税率汇总 (2020-11-19 11:43:09)
·《人力资源管理》关于时间和数字的考点汇总 (2020-11-16 7:31:38)
·《人力资源管理》关于时间和数字的考点(3) (2020-11-16 11:29:53)
·免费真题 ·模考试题


实用文档 | 入党资料 | 入党申请书 | 入党志愿书 | 个人自传 | 转正申请书 | 思想汇报 | 个人简历 | 简历模板 | 简历封面 | 工作计划 | 工作总结 | 自我评测
个性评测 | 社交评测 | 事业评测 | 运势评测 | 报告 | 实习报告 | 工作总结 | 社会实践 | 心得体会 | 述职报告 | 调查报告 | 辞职报告
法律文书 | 合同范本 | 演讲范文 | 更多>>
英语学习 | 听力口语 | 阅读写作 | 翻译文化 | 趣味英语 | 学习方法 | 英文经典歌曲 | 每日课堂 | 空中英语 | 少儿英语 | 影视英语 | 英文歌曲 | 更多>>
作文大全 | 作文 | 小学 | 初中 | 高中 | 话题作文 | 考研 | 四六级 趣味作文 | 体裁作文 | 记叙文 | 议论文 说明文 | 应用文 | 读后感 | 作文素材 | 名言警句
优美段落 | 哲理故事 | 诗词赏析 | 成语知识 | 技巧 | 写作指导 | 作文点评 | 佳文赏析 | 写作基础 | 话题演练 | 作文教学 | 更多>>



 下载
下载



































