第一章 资金时间价值与投资方案选择
历年考题分布
|
章节内容 |
年份 |
单选 |
多选 |
案例 |
合计 |
|
第一章资金时间价值与投资方案选择 |
2009 |
5 |
4 |
6 |
15 |
|
2010 |
5 |
4 |
8 |
17 | |
|
2011 |
5 |
4 |
8 |
17 | |
|
2012 |
5 |
2 |
4 |
11 | |
|
2013 |
5 |
4 |
10 |
19 |
本章内容框架

本章特点
考题所占分值大;
理论性强,技术含量高,难度大;
计算题多。
第一节 资金的时间价值
一、资金时间价值的概念
1.资金时间价值的含义
同一资金在周转使用过程中在不同时点上产生的价值差额。
2.资金时间价值变化的原因
(1)通货膨胀、货币贬值
(2)风险因素
(3)周转使用,货币增值
3.基本概念介绍
(1)利率(i) :相对数指标
(2)利息(I) :绝对数指标
(3)现值(P):货币的初始价值,即本金(期初金额)
(4)将来值(F):货币的未来价值,即本利和(未来值)
(5)年值(A):是指在一定的时期内,以相同的时间间隔连续发生的等额收付款项
二、资金时间价值的计算
1.单利制
利息和时间呈线性关系,利息不计入本金,计息基础不变,利息固定。(不能反映资金运动的规律性)
F本利和= P×(1+i×n)
2.复利制
是指不仅本金要计算利息,利息也要计算利息,即通常所说的? “利滚利”。 (符合资金时间价值的本质)
F本利和= P(1+i)n
应用分析
将3000元存入银行,年利率为5%,分别按单利、复利计算三年后的本利和为多少?
解:单利 F = P (1+i×n) =3000×(1+5%×3)=3000× 1.15=3450(元)
复利 F= P × (1+i)n = 3000 × (1+5%)3 =3000 × 1.158=3474(元)

3.现金流量图(辅助计算工具)
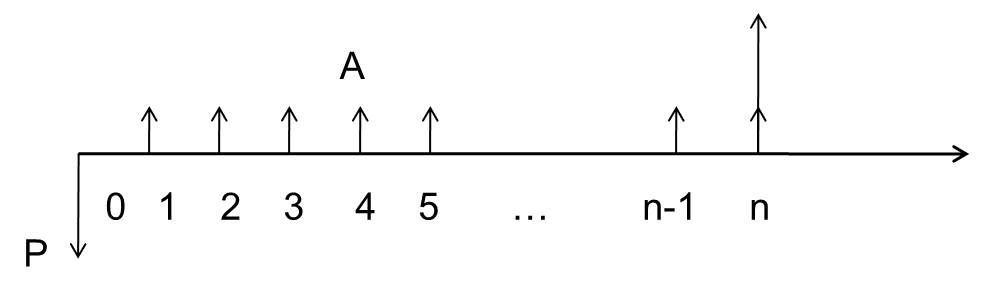
1.一条向右的带箭头的线代表时间轴
2.上面的点代表时间点,起点为0,依次为123…n
3.向上的箭头表示现金流入,向下的箭头代表现金流出
4.箭头的长短与资金量值成正比
4.现金流量计算的基本原则

(1)不在同一时点的资金不能比较大小
(2)不在同一时点的资金不能直接相加减
(3)只有将发生在各个点的资金量换算到同一时点,才能比较大小和相加减
5.基本系数
一次支付本利和因数(F/P,i,n)
一次支付现值因数(P/F,i,n)
等额支付将来值因数(F/A,i,n)
等额支付偿债基金因数(A/F,i,n)
等额支付现值因数(P/A,i,n)
等额支付资金回收因数(A/P,i,n)
1.一次性支付本利和公式
问题:已知现期的一个支付,在一定利率条件下,求未来某时点的将来值。即已知P、i、n,求F。图示如下:

这就是一般复利公式
应用分析
某夫妇喜得贵子之时,即投入一笔大学教育基金10000元,以年均5%的收益率投资,当孩子18岁上大学时,这笔基金会有多少呢?
解析:
F = 10000(F/P,5%,18)
= 10000×2.407
=24070(元)
2.一次性支付现值公式
问题:已知将来某个时点的一个支付,在一定利率条件下,求其现在值。即已知F、i、n,求P。图示如下:

它是一般复利公式的逆公式
应用分析
某夫妇喜得贵子之时,考虑投入一笔基金用于大学教育,预计孩子18岁上大学时所需各种费用为50000元,设年均收益率为8%,问现在应投入多少?
解析:?
P = 50000(P/F,8%,18)
= 50000×0.2502
= 12510(元)
3.等额支付将来值公式
问题:已知到将来某个时点的各期均有一个等额支付,在一定利率条件下,求其将来值。
即已知A、i、n,求F。图示如下:
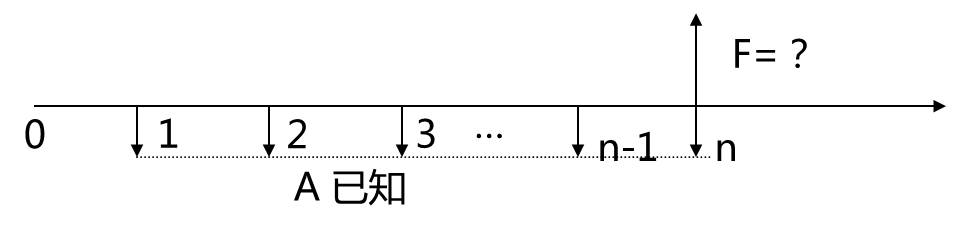

计算公式可由一般复利公式 F = P(1+ i) n推导出来
应用分析
某夫妇喜得贵子之时,考虑建立一项基金用于大学教育,计划每年注入2000元,至孩子18岁上大学时会有多少?设年均收益率为8%。
解析:
F = 2000(F/A,8%,18)
= 2000×37.45
= 74900(元)
4.偿债基金公式
问题:已知到将来某个时点的一个支付,在一定利率条件下,求从现在起到该时点各期的等额支付。即已知F、i、n,求A。图示如下:
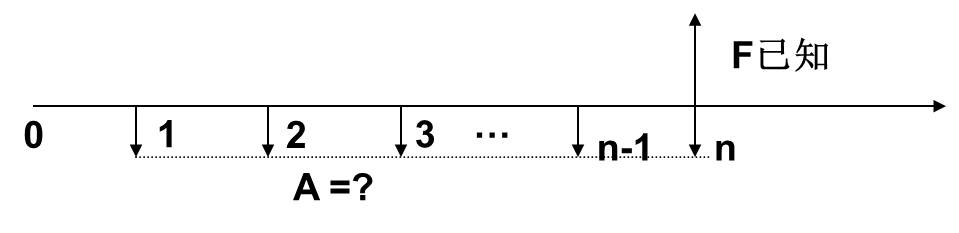

计算公式可由年金本利和公式推导而来
应用分析
某夫妇喜得贵子之时,考虑建立一项基金用于大学教育,预计孩子18岁上大学时所需各种费用为50000元,设年均收益率为8%,问从现在起每年应投入多少?
解析:
A = 50000(A/F,8%,18)= 50000×0.0267=1335(元)
5.等额支付现值公式
问题:已知到将来某个时点的各期均有一个等额支付,在一定利率条件下,求其现值。即已知A、i、n,求P。图示如下:


计算公式可由整付现值公式? P = F(1+ i)-n推导而来
应用分析
某人向建行申请10年期购房按揭贷款,他每年的还款能力为8000元,年利率为5%,问他可以向银行贷多少?
解析:
P = 8000(P/A,5%,10)
= 8000×7.722
=61776(元)
6.资金还原公式
问题:已知现在有一个支付,在一定利率条件下,求到将来某个时点各期的等额支付。即已知P、i、n,求A。图示如下:


计算公式可由年金现值公式推导出来
特殊情况当n→∞时 A=P·i
应用分析
某人向建行申请15年期购房按揭贷款12万元,年利率为5%,求他每年的还款额?
解析:
A = 120000(A/P,5%,15)
= 120000×0.09634
= 11560.8(元)
7.假定条件
(1)初期投资发生在方案的寿命期初;
(2)方案实施的经常性收益和费用假定发生在计息期的末期;
(3)本期的期末是下期的期初;
(4)现值P是当前期间开始时发生的;
(5)年值A是在考察期间间隔发生的;当问题包括P和A时,系列的第一个A是在P发生一个期间后的期末发生的;当问题包括F和A时,系列的最后一个A与F同时发生的。
8.解题步骤
第一步,审题。复杂题必须画出现金流量图帮助理解。(注意:现金流量图的三要素:大小 (现金数额)、方向(现金流入或流出)和作用点(现金发生的时间点)。一定要绘制正确。
第二步,确定换算关系。审题后确定其经济活动的内涵是哪两个值之间的换算,写出关系式,如A=P(A/P,i,n),这需要熟练掌握六种换算
第三步,审查条件。题中的条件与公式换算的假定条件是否一致,如不一致,则需调整换算关系式
第四步,检查一致性。注意i与n的内涵是否一致:如果i是年(季、月)利率,则n就是以年(季、月)为标准的计息期;如果没有明确告知,则季利率等于年利率除以4,月利率等于年利率除以12。
第五步,计算。将已知数据代入关系式中计算
应用分析
例1.有一对父母为两个孩子的大学教育攒钱。他们相差两岁,大的将在15年后上大学,小的则在17年后。估计届时每个孩子每年学费将达到21000元。年利率为10%,那么这对父母每年应存多少钱才够两个孩子的学费?现在起一年后开始存款,直到大孩子上大学为止。
A(F/A,15%,15)=21000×(P/A,15%,4)(1+15%)+21000×(P/A,15%,4)(P/F,15%,1)
故A=2544.87元
应用分析
例2. 某企业拟购买设备一台以更新旧设备,新设备价格较旧设备价格高出12000元,但每年可节约动力费用4000元,若利率为10%,请计算新设备应至少使用多少年对企业而言才有利。
(P/A,10%,3)=2.486
(P/A,10%,4)=3.169
4000(P/A,10%,n)=12000
(P/A,10%,n)=3 内插法:n=3.75
相关推荐:
- 培训课程
- 更多课程报名入口>>
在线课程 |
2024年
学考双赢定制班 63%学员选择 |
2024年
学考双赢黑卡班 31%学员选择 |
2024年
学考双赢取证班 6%学员选择 |
2024年
专项提分班 |
||
| 学 | 基础学习 拿分阶段 |
私教精讲班 | ||||
| 强化学习 提分阶段 |
重要考点提炼班 | |||||
| 练 | 冲刺密训 抢分阶段 |
8套名师密押卷 | ||||
| 背 | 考前终极 抢分阶段 |
通关必备200题 | ||||
| 考前3小时密训班 | ||||||
| 专项班 | 经济基础: 图形/计算题专项 |
|||||
| 专业课: 案例专项专项 |
||||||
| ★★★ 三星题库 ¥680/年 |
每日一练 |
|||||
每日错题榜 |
||||||
章节刷题 |
||||||
| ★★★★ 四星题库 ¥980/年 |
真题题库 |
|||||
高频常考 |
||||||
大数据易错 |
||||||
| ★★★★★ 五星题库 ¥1680/年 |
通关必备200题 |
|||||
名师密押8套卷 |
||||||
| 教学资料 | 课程讲义 | |||||
| 全程学习计划书 | ||||||
| 人工助学服务 | 微信一对一 班主任督学 7×13陪伴模式 |
|||||
| 老师微信 一对一答疑 |
||||||
| 定制服务 无忧从容包 |
无忧从容卡 ¥980 | |||||
| 专项突破班 ¥1360 | ||||||
| 黑卡特权 | 不过退费 | |||||
| 额外赠送 | 赠送2023年 【教材精讲班】 |
赠送2023年 【教材精讲班】 |
赠送2023年 【教材精讲班】 |
|||
| 课程有效期 | 2024年11月30日 | 2025年11月30日 | 2024年11月30日 | 2024年11月30日 | ||
| 套餐价格 | 全科:¥4680 单科:¥2880 |
全科:¥9880 单科:¥5980 |
全科:¥1580 单科:¥880 |
全科:¥1080 单科:¥680 |
||
·2020年中级经济师《工商管理》考试大纲 (2020-04-13 11:47:57)
·2020年中级经济师《财政税收》考试大纲 (2020-04-13 11:47:54)
·2020年中级经济师《农业经济》考试大纲 (2020-04-13 10:14:39)
·2020年中级经济师《金融专业》考试大纲 (2020-04-13 11:47:52)
·2020年中级经济师《保险专业》考试大纲 (2020-04-13 10:14:25)
·免费真题 ·模考试题


实用文档 | 入党资料 | 入党申请书 | 入党志愿书 | 个人自传 | 转正申请书 | 思想汇报 | 个人简历 | 简历模板 | 简历封面 | 工作计划 | 工作总结 | 自我评测
个性评测 | 社交评测 | 事业评测 | 运势评测 | 报告 | 实习报告 | 工作总结 | 社会实践 | 心得体会 | 述职报告 | 调查报告 | 辞职报告
法律文书 | 合同范本 | 演讲范文 | 更多>>
英语学习 | 听力口语 | 阅读写作 | 翻译文化 | 趣味英语 | 学习方法 | 英文经典歌曲 | 每日课堂 | 空中英语 | 少儿英语 | 影视英语 | 英文歌曲 | 更多>>
作文大全 | 作文 | 小学 | 初中 | 高中 | 话题作文 | 考研 | 四六级 趣味作文 | 体裁作文 | 记叙文 | 议论文 说明文 | 应用文 | 读后感 | 作文素材 | 名言警句
优美段落 | 哲理故事 | 诗词赏析 | 成语知识 | 技巧 | 写作指导 | 作文点评 | 佳文赏析 | 写作基础 | 话题演练 | 作文教学 | 更多>>


 下载
下载



































