| 第 1 页:货币的时间价值 |
第四章 价值评估基础
考点:货币的时间价值
【内容导航】
1.货币时间价值的基础知识
2.一次性款项的现值和终值
3.普通年金的终值与现值
4.预付年金的终值与现值
5.递延年金
6.永续年金
7.报价利率、计息期利率和有效年利率——年内多次计息情况
【考频分析】
考频:★★★
复习程度:需要掌握各种终值和现值的计算。
【主要考点】货币的时间价值
1.货币时间价值基础知识
| 含义 | 货币时间价值是指货币经历一定时间的投资和再投资所增加的价值,也称为资金时间价值。 |
| 终值与现值的概念 | 1.终值又称将来值,是现在一定量现金在未来某一时点上的价值,俗称“本利和”,通常记作F。 2.现值,是指未来某一时点上的一定量现金折合到现在的价值,俗称“本金”,通常记作“P”。 |
| 利息计算方法 | 单利:只对本金计算利息。 复利:不仅要对本金计算利息,而且对前期的利息也要计算利息。 |
2.一次性款项的现值和终值
| 单利终值与现值 | 单利终值:F=P+P×i×n=P×(1+i×n) | 单利现值系数与单利终值系数互为倒数 |
| 现值的计算与终值的计算是互逆的,由终值计算现值的过程称为“折现”。单利现值的计算公式为:P=F/(1+n×i) | ||
| 复利终值与现值 | 复利终值公式: F=P×(1+i)n 其中,(1+i)n称为复利终值系数,用符号(F/P,i,n)表示 |
复利现值系数(P/F,i,n)与复利终值系数(F/P,i,n)互为倒数 |
| 复利现值 P=F×(1+i)-n 其中(1+i)-n称为复利现值系数,用符号(P/F,i,n)表示 |
3.普通年金的终值与现值
(1)普通年金终值==(复利终值系数--1)/i
(2)普通年金现值系数==(1--复利现值系数)/i
【提示】偿债基金现值系数和普通年金终值系数互为倒数关系;资本回收系数与普通年金现值系数互为倒数关系。
4.预付年金终值与现值
(1)预付年金终值
即付年金的终值,是指把预付年金每个等额A都换算成第n期期末的数值,再来求和。
具体有两种方法:
方法一:F=A[(F/A,i,n+1)-1]
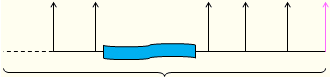
(1)按照n+1期的普通年金计算终值;,
(2)再把终值点的年金去掉.
【提示】预付年金终值系数与普通年金终值系数的关系:期数加1,系数减1.
方法二:预付年金终值=普通年金终值×(1+i)。
(2)预付年金现值
具体有两种方法:
方法一:P=A[(P/A,i,n-1)+1]

【提示】预付年金现值系数与普通年金现值系数的关系:系数加1,期数减1.
方法二:预付年金现值=普通年金现值×(1+i)
5.递延年金
递延年金,是指第一次等额收付发生在第二期或第二期以后的年金。图示如下:
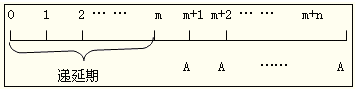
M——递延期,n——连续支付期
(1)递延年金终值计算
计算递延年金终值和计算普通年金终值类似。
F=A×(F/A,i,n)
【注意】递延年金终值只与连续收支期(n)有关,与递延期(m)无关。
![]()
(2)递延年金现值的计算
【方法1】两次折现
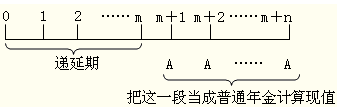
计算公式如下:
P=A(P/A,i,n)×(P/F,i,m)
【方法2】年金现值系数之差
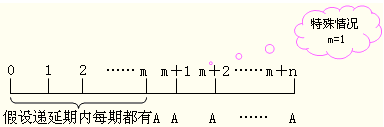
计算公式如下:
P=A(P/A,i,m+n)-A(P/A,i,m)=A[(P/A,i,m+n)-(P/A,i,m)]
6.永续年金
永续年金,是指无限期等额收付的年金。
永续年金因为没有终止期,所以只有现值没有终值。永续年金现值==A/I。
7.报价利率、计息期利率和有效年利率——年内多次计息情况
| 报价利率 | 报价利率是指银行等金融机构提供的利率。 在提供报价利率时,还必须同时提供每年的复利次数(或计息期的天数),否则意义是不完整的。 |
| 计息期利率 | 计息期利率是指借款人每期支付的利息与本金的百分比,它可以是年利率,也可以是六个月、每季度、每月或每日等。 计息期利率=报价利率/每年复利次数 |
| 有效年利率 | 有效年利率,是指在按给定的计息期利率每年复利次数计算利息时,能够产生相同结果的每年复利一次的年利率,也称等价年利率。
有效年利率的推算: 式中,r——报价利率 m——每年复利次数 i——有效年利率 |

关注"566注册会计师"微信,第一时间获取最新资讯、试题、内部资料等信息!
注册会计师题库【手机题库下载】| 微信搜索"566注册会计师"
| 注册会计师QQ群: |
|---|
相关推荐:
·2018年注册会计师考试《公司战略》备考资料(29) (2018-06-29 16:29:30)
·2018注册会计师考试《财务管理》知识点精讲(30) (2018-06-29 16:28:21)
·2018注册会计师考试《财务管理》知识点精讲(29) (2018-06-29 16:23:30)
·2018年注册会计师考试《经济法》要点概论(30) (2018-06-29 16:19:53)
·2018年注册会计师考试《经济法》要点概论(29) (2018-06-29 16:06:47)
实用文档 | 入党资料 | 入党申请书 | 入党志愿书 | 个人自传 | 转正申请书 | 思想汇报 | 个人简历 | 简历模板 | 简历封面 | 工作计划 | 工作总结 | 自我评测
个性评测 | 社交评测 | 事业评测 | 运势评测 | 报告 | 实习报告 | 工作总结 | 社会实践 | 心得体会 | 述职报告 | 调查报告 | 辞职报告
法律文书 | 合同范本 | 演讲范文 | 更多>>
英语学习 | 听力口语 | 阅读写作 | 翻译文化 | 趣味英语 | 学习方法 | 英文经典歌曲 | 每日课堂 | 空中英语 | 少儿英语 | 影视英语 | 英文歌曲 | 更多>>
作文大全 | 作文 | 小学 | 初中 | 高中 | 话题作文 | 考研 | 四六级 趣味作文 | 体裁作文 | 记叙文 | 议论文 说明文 | 应用文 | 读后感 | 作文素材 | 名言警句
优美段落 | 哲理故事 | 诗词赏析 | 成语知识 | 技巧 | 写作指导 | 作文点评 | 佳文赏析 | 写作基础 | 话题演练 | 作文教学 | 更多>>



 下载
下载






