2018事业单位行测技巧：数量关系之质合数

　　在事业单位考试中，数论关系是整个数学运算的基础，只有打好基础才能做好数学运算的题目，而数论关系中的质合数是非常重要的知识点之一，可以单独做考点，同时也与公约数公倍数相关联，下面我们来学习一下质合数。

　　1、质合数的基本概念

　　质数：一个大于1的自然数如果只有1和它本身两个因数，这样的数叫做质数。如：2、3、5、7都是质数，质数有无限多个，最小的质数是2。

　　合数：一个自然数如果除了1和它本身还有别的因数，这样的数叫做合数。如：4、6、15、49都是合数，合数也有无限多个，最小的合数是4。

　　2是唯一的偶质数，1既不是质数也不是合数。

　　2、质数判定方法

　　(第一步)判断自然数A是不是质数，要找到比A大的最小的平方数。

　　(第二步)将小于这个平方数的平方根的所有质数找出来。

　　(第三步)如果A不能够被(第二步)中提到的所有质数整除，那么A就是质数。如果A能够被(第二步)中提到的至少一个质数整除，那么A就是合数。

　　例如：判断251是否是质数。

　　(第一步)251<256=142

　　(第二步)小于14的质数有：2、3、5、7、11、13

　　(第三步)由于251不能被2、3、5、7、11、13整除，所以251是质数。

　　3、合数的判定方法

　　根据质数判定方法中的(第三步)中所提到的“如果A能够被(第二步)中提到的至少一个质数整除，那么A就是合数。”

　　4、分解质因数

　　(1)定义：每个合数都可以写成几个质数相乘的形式，把一个合数分解成若干个质因数乘积的形式，叫做分解质因数。

　　(2)方法：短除法。

　　5、分解质因数的应用

　　(1)求正约数的个数：

　　分解质因数法求正约数个数的方法：质因数指数加1后相乘。　　

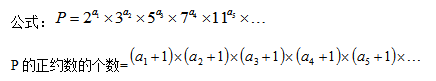
　　(2)利用拆分找突破口：题目中直接或间接的给出乘积关系

　　(3)特征数字的因式分解

　　第一步：找到特征数字的循环节数字。

　　第二步：将每个循环节数字中的最后一位变成1，其余数字都变。

　　6、习题应用

　　例题1：学校准备了1152块正方形彩板，用它们拼成一个长方形，有多少种不同的拼法?

　　A.52 B.36 C.28 D.12

　　【答案】D

　　【解析】长方形的长和宽相乘即为面积，假设一块正方形的边长为1，那么1152即为长方形的面积，1152就等于长乘以宽，所以把1152进行拆分既是长和宽的不同情况。1152=27×32，有(7+1)×(2+1)=24个正约数，可以凑成12组乘积组合，因此选择D。

　　例题2：四个连续自然数的积是3024，则这四个数的和是多少?

　　A.28 B.30 C.33 D.40

　　【答案】B

　　【解析】已知四个连续自然数的乘积想求这四个数的和，可以利用拆分找突破口。3024=24×33×7，因为是四个连续的自然数，因此为6×7×8×9，加和为30，因此选择B。

　　以上为质合数的知识点，希望对大家有所帮助。

扫描/长按二维码可帮助公考通关

获取2019年公务员报名

下载公务员职位表下载

获取公务员面试公告

获取历年公考真题试卷

公务员万题库下载｜ 微信搜"万题库公务员考试"

　　相关推荐：

　 　各地2018年事业单位考试费用汇总