2019上海事业单位行测技巧：特值法解交替合作问题

　　在公职行测数量关系部分有很多题型，比如近几年比较热的工程问题。工程问题题型很多，包括普通工程问题、多者合作问题、交替合作问题和多劳力合作问题等。虽然题型很多，但每一种题型的解题方法规律性很强，只要确定好对应题型，按照规律即可快速求解。特值法应用范围很广，只要符合或可以转换为M=A×B这种形式，当求其中一个量时，另外两个量未知，我们可以结合题干信息采用特值法解题。那么我们今天就给大家介绍交替合作的题型特征及如何应用特值法求解交替合作问题。

　　一、题型特征

　　一项工作以交替合作的方式完成，即轮流循环的工作模式进行即为交替合作。

　　二、解题思路

　　例题：一项工程，甲单独12小时，乙单独16小时，甲、乙合作按甲、乙，甲、乙，甲、乙…的工作顺序，每人各1小时，轮流工作，问完成时用多少天?。

　　A.13小时30分钟 B.13小时40分钟 C.13小时45分钟 D.14小时

　　答案：B。解析：“按甲、乙，甲、乙，甲、乙…的工作顺序，每人各1小时”典型的交替合作问题。“一项工程”工作总量固定，求时间，对应工作量和效率均未知，因此可以用设特值的方法求解。工作总量固定，可设工作总量为特值，结合题干中12小时、16小时，可设工作总量为时间的公倍数48，表示出甲和乙的效率分别为4和3;循环交替工作，如果知道一个循环周期的工作量即可求得需要多少的循环周期，结合题干知一个循环甲乙各工作1小时，共计工作2小时，结合上一步知2小时的工作量为7;求出有多少循环周期即可求出时间，总工作量W总=48，由48÷7=6……6知需要6个循环还余下6份工作量;　　

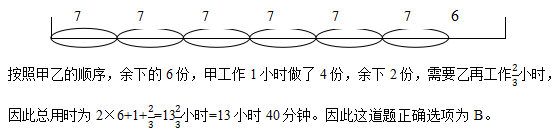
　　正效率交替合作求解思路总结：

　　1、已知时间，工作总量固定，设总量为特值，设“时间们”的(最小)公倍数为特值，表示各自出效率;

　　2、找循环规律：求一个周期内工作量W一个循环和工作时间T一个循环;

　　3、求周期数，看剩余工作量，周期个数N=W总÷W一个循;

　　4、求时间：分配剩余工作量，求时间。

　　例题： 有一蓄水池，池中有一条进水管和一条排水管，灌满一池水需要打开进水管2小时，排光一池水需打开排水管5小时。水池原先为空，如果按照进水、排水、进水、排水…的顺序轮流各开1小时，多长时间住满?

　　A.4小时 B.4.8小时 C.5.4小时 D.6.2小时

　　答案：B。解析：“按照进水、排水、进水、排水…的顺序轮流各开1小时”典型的交替合作问题。一池水量固定，求多长时间灌满，对应水池量和进排水效率均未知，因此可以用设特值的方法求解。结合题干中5小时、2小时，可设水池蓄水量为10，表示出进水和出水的效率分别为5和-2;一个循环周期内工作时间为2小时，工作量为5+(-2)=3;求循环周期10÷3=3……1，理论上经过3个循环还余下1份水没灌满，还需要0.2小时，总时间2×3+0.2=6.2小时，但是具体实际操作如果按照理论上来相当于两个循环后，再进水5，其中有1份漏出来后满了，此时再排出2份水，还需要注入1份水，整个过程并不是最少时间。要想得时间为实际的最少时间，不妨先假设最后一次进水量最大为5，则前边需进水5，需要5÷3≈1.7个周期，向上取整，即需要2个周期，那么假设的5其实在实际中进水为10-2×3=4份，这4份水用时0.8小时，总时间2×2+0.8=4.8小时才是实际中最少的时间。因此这道题正确选项为B。　　

　　正负效率同在交替合作求解思路总结：

　　1、已知时间，工作总量固定，设总量为特值，设“时间们”的(最小)公倍数为特值，表示各自出效率;

　　2、找循环规律：求一个周期内工作量W一个循环和工作时间T一个循环;

　　3、求周期数：用工作总量减去周期峰值后除以周期工作量，结果向上取整，求出周期数和剩余工作量;

　　4、求时间：分配剩余工作量，求时间。

　　通过上面的讲解相信大家对工程问题——交替合作有了了解，希望同学后续多加练习快速掌握，为后期解交替合作奠定基础。