2014广东公务员数学运算最新命题趋向及考点预测

　　二、几何问题的新思维、新变化

　　几何问题是近年来国考数量关系的常考重点题型，题量维持在2道左右。且近几年国考中的几何问题的出题方式也不再局限于传统知识点的考查，更多的是考查考生的思维能力以及解决新题型的能力。因此，考生在备考过程中应对该问题引起足够的重视，做足充分准备，熟悉常考题型及常见解题思路，并且灵活运用基本方法解决新题型。当遇到使用常规思路和解题方法无法解决的问题时，考虑在时间充裕的情况下发散思维，多种角度思考该问题，找到快速的解题方法。

　　结合历年考查，几何问题不断求变、求新，因此，广东公务员考试网给出以下三道新颖的几何问题，其一为2013年国考压轴题。考生需要认识到：几何问题无论如何变化，其解决方法认识从基本公式、基本知识点入手。

　　【例】(2013国家-75)若干个相同的立方体摆在一起，前、后、左、右的视图都是

　　，问这堆立方体最少有多少个?

　　A.4 B.6　　C.10 D.8

　　【解析】四个正方体如下图摆放，即在“九宫格”的对角线上各摆放一个正方体，再在中心正方体的上方放置一个正方体。左图为立体图，右图为其四向视图。

　　【预测题目1】如下图所示，在用多边形对平面进行密铺时，相拼接的边相等，每个拼接点处各个角的和为360°，我们称其可以完成平面密铺。那么一下哪种图形不能单独完成平面密铺?

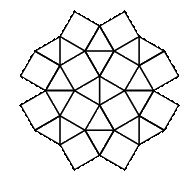
　　A正三角形 B正方形

　　C正六边形 D正八边形

　　分析：很多考生拿到此题后觉得无从下手，仿佛我们从未接触过此类题型。什么是平面密铺?概念很陌生，但是我们只要仔细读题、认真看图后就不难发现：所谓平面密铺，只需满足两个条件，结合所给图示：①正方形和与之拼接的正三角形的边长相等;②每个交点处，正方形和正三角形的各内角和为360°(每个交点处有3个正三角形的内角及2个正方形的内角：3×60°+2×90°=360°)。而题目所求为：只使用一种图形的平面密铺，因此，我们只需考虑以上两个条件即可。显然，只采用一种图形，其对应的拼接边长必然相等;而欲使每个交点处的内角和为360°，由于对于单一正多边形，其每个内角度数相等，因此，只需其内角度数为360°的约数即可，正三角形、正方形、正六边形、正八边形的内角度数分别为，60°、90°、120°、135°，因此正八边形无法单独实现平面密铺。因此，本题答案选择D选项。

　　小结：本题表面上为几何问题，但实质考查的知识点为约数倍数，是我们很熟悉的一个考点。因此，在解决此类几何问题时，我们需要冷静分析，仔细审题，拨开浓雾，方见彩虹。

　　【预测题目2】已知图中的三角形均为直角三角形，且三边长度均为整数，正方形ABCD的面积为1平方厘米，那么正方形EFGH的面积为正方形ABCD的多少倍?( )

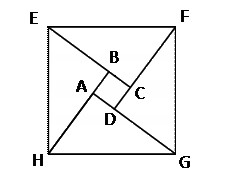
　　A.10 B.5

　　C.25 D.12

　　分析：读题之后，我们发现题目所给的数据量很少，似乎难以求解，但是仔细看图后不难发现，由于图中所有三角形均为直角三角形，我们易证四个直角三角形是全等的(对应角相等，且斜边相等)。因此，由正方形ABCD的面积为1平方厘米，可知正方形ABCD的边长为1厘米，因此，两直角边长度相差1，又三边长度均为整数可知图中直角三角形三边长为3、4、5，因此正方形EFGH的面积为5×5=25平方厘米，为正方形ABCD的25倍。因此，本题答案选择C选项。

　　小结：本题亦是考查分析解决新问题的典型示例，实质上考查了三角形全等和常见的勾股数，与上一个例题类似，考生们只要冷静分析，结合所学知识点和基本公式，对于此类几何问题是可以很好的解决的。

　　三、溶液问题：考查饱和溶液的概念

　　历年国考对于溶液问题都有或多或少的考查，今年也不会例外。而溶液问题的传统题型各位考生在备考过程中也应做好充分的准备，在此我就不进行过多的介绍了。我们需要重点关注的溶液问题的题型是考查饱和溶液，可能部分考生对于此概念还是比较陌生的。因此，我们结合两道例题进行说明：

　　【例】(安徽2012-62)在某状态下，将28g某种溶质放入99g水中恰好配成饱和溶液，从中取出1/4溶液加入4g溶质和11g水，请问此时浓度变为多少?( )

　　A. 21.61% B. 22.05% C. 23.53% D. 24.15%

　　分析：读完题目后可能部分考生就直接拿笔开始计算了，给出了溶质和溶剂质量，求解溶度，很常规的题目。但实际上呢，我们仔细审题后发现，初始溶液已达饱和，而所加的4g溶质和11g水，直接计算浓度的话是大于初始浓度的，而初始溶液已达饱和，也就是说无法溶解更多的溶质，那么加入4g溶质和11g水之后浓度应该与饱和时的浓度相同，即28÷(28+99)=22.05%。因此，本题答案选择B选项。

　　【例】现有一定浓度的盐水若干克，蒸发一定量的水之后溶液浓度变为20%，在蒸发同样多的水之后浓度变为25%，在蒸发同样多的水之后浓度变为26.5%。那么再蒸发同样多的水之后浓度变为多少?( )

　　A.26.5% B.30% C.33% D.35%

　　分析：初看本题，很多考生误以为是传统的等溶质增减类题目，但是稍加计算后发现：由于溶质含量固定，因此每次蒸发同样多的水后，浓度的变化量应该变大，而第三次蒸发后，浓度的变化量为1.5%<5%，说明溶液在第三次蒸发后已变为饱和溶液，因此再次蒸发后浓度应为26.5%。因此，本题答案选择A选项。

　　小结：以上两道例题均考查了饱和溶液的概念，考生只需记住，在一定条件下，溶液若达到饱和，无论在添加多少溶质，其浓度均不会发生改变。此类题型只要不落入题中设置的陷阱，其难度是远远小于传统浓度问题的。

　　四、基础题型保持相对稳定

　　除了以上国考变化的新趋势，国考考查的热点还有相当一部分集中在传统题型上：如典型的行程问题、工程问题、容斥问题、最值问题(需要特殊说明的是;最值问题在近年的考查重点逐步转移到了构造数列问题上，考生需要引起注意)、排列组合问题、和差倍比问题，以上这些考点的考查大多偏向常规题型，考生们只需掌握基本公式和基本解题方法便能应对自如。

　　结语：结合考试大纲和历年真题，我们发现数学运算部分的考查趋向于基础题型和新题型结合的考查方式，且新题型所占比重不是很大。而且无论题目再怎么创新，其核心和基础的公式不会改变，追根溯源依然是考查我们最基本的知识点。因此，广大考生在复习备考过程中，只有注意传统与创新的结合，夯实基础，，才能不惧创新题型，把握好综合性题型。祝大家一举成“公”。

　　相关推荐：

　　2014广东公务员将考试行测备考:剖析四大矛盾

　　2014广东公务员行测备考：统计表资料分析精讲

　　2014广东公务员行测备考：文字资料分析题型介绍