文章责编：zhangguojuan
看了本文的网友还看了学历| 高考 中考 考研 自考 成考 外语| 四六级 职称英语 商务英语 公共英语 资格| 公务员 报关员 银行 证券 司法 导游 教师 计算机| 等考 软考
工程|一建 二建 造价师 监理师 咨询师 安全师 结构师 估价师 造价员 会计| 会计证 会计职称 注会 经济师 税务师 医学| 卫生资格 医师 药师 [更多]
几何问题一般涉及几何图形的边长、周长、表面积、体积等相关变量，其中最基础的一类题型，就是关于规则基本图形(三角形、长方形、正方形、圆形、扇形、球体、柱体、锥体等)直接的计算问题。另外，还有很多题目是依靠重要的“几何特性”完成答题的，而这些几何特性也成为近几年来考查的热点。
历年真题：
【2013年国考】75.若干个相同的立方体摆在一起，前、后、左、右的视图都是
A.4 B.6
C.8 D.10
【2012年421联考】52.某公司要在长、宽、高分别为50米、40米、30米的长方体建筑的表面架设专用电路管道联接建筑物内最远两点，预设的最短管道长度介于： 几何问题
A. 70—80米之间 B. 60—70米之间
C. 90—100米之间 D. 80—90米之间
【2012年山东】60. 木工师傅为如图所示的3层模具刷漆，每层模具分别由1、3、6个边长1米的正方体组成。如果用一公斤漆可以刷20平方米的面积。那么为这个3层模具的所有外表面上色，需要几公斤漆?( )几何构造问题?
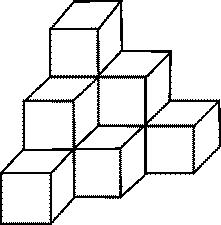
A. 1.8 B. 1.6
C. 1.5 D. 1.2
【2013年联考】54.连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米，问正八面体的体积为多少立方厘米? 几何问题
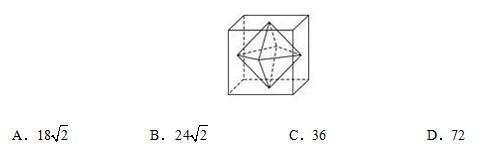
【2012年915联考】61.气象台测得在S岛正东方向80千米处，一台风中心正以20千米/小时的速度沿北偏西60度的方向匀速移动。若台风中心50千米范围内为影响区域，台风中心移动方向不变、强度不变，该台风对S岛的影响时间约持续：几何计算
A.2小时 B.3小时
C.4小时 D.5小时
【2010年918联考】长方形ABCD的面积是72平方厘米，E、F分别是CD、BC的中点，三角形AEF的面积是多少平方厘米? 几何问题
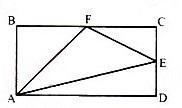
A. 24 B. 27
C. 36 D. 40
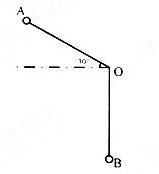
【2010年918联考】长为1米的细绳上系有一个小球，从A处放手以后，小球第一次摆到最低点B处共移动了几米?几何问题
A. 1+1/3π B. 1/2+1/2π
C. 2/3π D. 1+2/3π
【2013年国考】62.阳光下，电线杆的影子投射在墙面及地面上，其中墙面部分的高度为1米，地面部分的长度为7米。甲某身高1.8米，同一时刻在地面形成的影子长0.9米。则该电线杆的高度为( )几何计算
A.12米 B.14米
C.15米 D.16米
【2012年915联考】53. 某厂生产一批商标，形状为等边三角形或等腰三角形。已知这批商标边长为2cm或4cm，那么这批商标的周长可能是：几何特性
A. 6cm 12cm B.6cm 8cm 12cm
C. 6cm l0cm 12cm D. 6cm 8cm l0cm 12cm
【2012年421联考】59. A、B两地直线距离40千米，汽车P与两地直线距离和等于60千米。则以下判断正确的是： 几何特性
A. 如果A、B、P不在同一条直线上，汽车所在位置有3个，可位于A、B两地之间或A、B两地外侧
B. 如果A、B、P不在同一条直线上，汽车的位置有无穷多个
C. 如果A、B、P位于同一条直线上，汽车拉于A、B两地之间或两地外侧
D. 如果A、B、P位于同一条直线上，汽车位于A、B两地外侧，且汽车到A的距离为20千米
【2010年425联考】一个正三角形和一个正六边形周长相等，则正六边形面积为正三角形的：几何特性
A.
C.
从上面一些历年真题可以知道，大部分几何图形都可以通过公式法和几何特性法来解决，但是也有一部分的几何题型是“不规范”的，或者利用公式求解较为麻烦的，这时候就需要我们利用“割补平移”的思想来求解。所以考生在复习几何问题的时候，尤其碰到不规则图形求周长、体积、表面积时，一定要有这种“割补平移”的思想去解答几何问题。几何问题属于必考题型，属于9道基础题型，所以希望广大考生好好复习。
