文章责编：zhangguojuan
看了本文的网友还看了学历| 高考 中考 考研 自考 成考 外语| 四六级 职称英语 商务英语 公共英语 资格| 公务员 报关员 银行 证券 司法 导游 教师 计算机| 等考 软考
工程|一建 二建 造价师 监理师 咨询师 安全师 结构师 估价师 造价员 会计| 会计证 会计职称 注会 经济师 税务师 医学| 卫生资格 医师 药师 [更多]
2006年
39. A、B两地以一条公路相连。甲车从A地，乙车从B地以不同的速度沿公路匀速率相向开出。两车相遇后分别掉头，并以对方的速率行进。甲车返回A地后又一次掉头以同样的速率沿公路向B地开动。最后甲、乙两车同时到达B地。如果最开始时甲车的速率为X米/秒，则最开始时乙车的速率为( )。
A. 4X米/秒 B. 2X米/秒 C. 0.5X米/秒 D. 无法判断
【解析】
答案：B。树形结合解题，画出线段图如下图所示。用V甲表示甲车最开始的速度、以V甲速度行驶的路程用实线表示;用V乙表示乙车最开始的速度，以V乙速度行驶的路程用虚线表示。
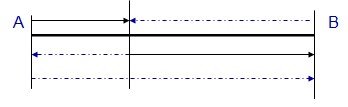
认真观察线段图，可以看出，相同时间内，以甲车速度V甲行驶的路程为1个AB全程，以乙车速度V乙行驶的路程为2个AB全程。因此，时间相等，V乙：V甲=路程之比=2AB:1AB=2:1，即V乙 = 2V甲 = 2x。
2007年
53. A、.B 两站之间有一条铁路，甲、乙两列火车分别停在 A 站和 B 站，甲火车 4 分钟走的路程等于乙火车 5 分钟走的路程.乙火车上午8 时整从B 站开往A站，开出一段时问后，甲火车从 A 站出发开往 B 站，上午 9时整两列火车相遇.相遇地点离A、.B两站的距离比是15：16.那么.甲火车在( ) 从 A 站出发开往 B 站.
A. 8时12 分 B. 8时15 分 C. 8 时 24 分 D. 8 时 30 分
【解析】
答案：B。此题考查比例和相遇问题。根据题意，s相同，V甲与V乙之比与时间成反比，则V甲：V乙=5:4。设乙的速度为4份/时，相遇时，乙刚好行驶了1个小时，共行驶4份的路程。假设，相遇时，甲时间行驶的路程为X份，则甲、乙行驶路程之比S甲：S乙=15：16 = x :4，则x = 15/4份，相遇时甲行驶时间t甲 = 15/4 ÷5 = 3/4小时=45分钟。甲行驶了45分钟，因此，甲在8点15分从A站出发开往B站。
2009年
119.某市水库水量的增长速度是一定的，可供全市12万人使用20年，在迁入3万人之后，只能供全市人民使用15年，市政府号召大家节约用水，希望将水库的使用寿命延长至30年，那么居民平均需要节约用水量的比例是多少?( )
A. 2/5 B. 2/7 C. 1/3 D. 1/4
【解析】
答案：A。牛吃草问题，转化为追及问题。设每年每万人用水速度为1，降水量的速度为V，设节水后用水速度为X，根据水库的存水量不变，列出方程。(12 —V)×20 = (15 —V)×15 = (X —V)×30，解得V = 3，X = 9，未节水以前用水速度为15，节水15 – 9 = 6，节水比例为6/15 = 2/5.选A。
2010年
54、某旅游部门规划一条从甲景点到乙景点的旅游线路，经测试，旅游船从甲到乙顺水匀速行驶需3小时;从乙返回甲逆水匀速行驶需4小时。假设水流速度恒定，甲乙之间的距离为y公里，旅游船在净水中匀速行驶y公里需要x小时，则x满足的方程为：
A. 1/(4-X)=1/X +1/3 B. 1/(3+X)=1/4 + 1/ X
C. 1/3 -1/X=1/4 + 1/X D. 1/3 -1/X =1/X -1/4
【解析】
答案：A。流水行船问题。 根据流水行船公式：水速=(顺水速度-逆水速度) /2.。应用特值法，设y=1，则1/X=1/3 -1/4) /2 ，移项变形后为 1/3 -1/X =1/X -1/4。选A。
2011年
68.甲、乙两人在长30米的泳池内游泳，甲每分钟游37.5米，乙每分钟游52.5米，两人同时分别从泳池的两端出发，触壁后原路返回，如是往返。如果不计转向的时间，则从出发开始计算的1分50秒内两人共相遇了多少次?
A.2 B.3 C.4 D.5
【解析】
答案：B。走完一个全程30米，甲、乙相遇的时间为30/(37.5+52.5)= 1/3分钟=20秒，根据多次相遇结论，甲乙第一次、第二次、……、第n次相遇的时间比为1:3：……：2n-1，可知当行驶时间为1分50秒及110秒时，(2n-1)*20≤110，解得n≤3.25，因此相遇了3次，还在第3次相遇后往第4次相遇的途中。此题亦可结合路程比为甲乙第一次、第二次、……、第n次相遇时分别行驶的总路程比为1:3：……：2n-1来解题。
2012年
69.一只装有动力桨的船，其单靠人工划船顺流而下的速度是水速的3倍。现该船靠人工划动从A地顺流到达B地，原路返回时只开足动力桨行驶，用时比来时少2/5。问船在静水中开足动力浆行驶的速度是人工划船速度的多少倍?()
A. 2 B. 3 C. 4 D. 5
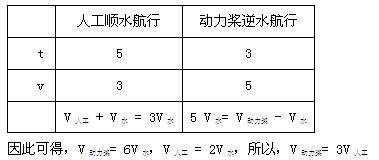
【解析】答案：B。根据题干条件，应用比例法、列表法。人工顺水与动力桨逆水的时间比为1：(1-2/5)=5:3
2013年
70.某河段中的沉积河沙可供80人连续开采6个月或60人连续开采10个月。如果要保证该河段河沙不被开采枯竭，问最多可供多少人进行连续不问断的开采(假定相对稳定)( )
A.25 B.30 C.35 D.40
【解析】
答案：B。牛吃草问题，转化为追及问题求解。假设每人每月开采的沉积河沙的速度为1，也就是每人每月开采河沙的量为1份，设该河段河沙每月的沉积速度为x，也就是该河段河沙每月的沉积量为x份，根据该河段原有沉积河沙量相等，列方程 (80 – x )×6 = ( 60-x ) ×10，解得x = 30。要保证该河段河沙不被开采枯竭，则每月所有人累计开采的河沙量不能超过该河段河沙的每月的沉积量，即最多不能超过30，因此最多不超过30÷1=30人。
相关推荐：
