2015年国家公务员《行测》数量关系专项练习(1)

　　查看汇总：2015年国家公务员《行测》数量关系专项练习汇总

　　1( 单选题 )某商店2万元购进一批商品，按原价卖出这批商品的五分之二后，由于市场情况发生变化，决定以七五折销售所剩商品，等商品全部卖出后结算发现这批商品亏损2000元，则降价前这批商品的利润率约为()

　　A. 6%

　　B. 7%

　　C. 8%

　　D. 9%

　　答案： A， 来源：陕西2013

　　考点：利润率折扣类

　　解析：假设进了100件货，单价200元，定价X。则有

　　因此，本题答案为A选项。技巧赋值法

　　2( 单选题 )

　　五名工人按甲—乙—丙—丁—戊的顺序轮流值夜班，每人值班1天休息4天。某日乙值夜班，问再过789天该谁值班?

　　A. 甲

　　B. 乙

　　C. 丙

　　D. 戊

　　答案： A， 来源：山西2014

　　考点：周期给定类

　　解析： 题目当中提到五名工人循环值夜班，因此是5个人是一个周期，789除以5得157余4。每过5个人又是轮到乙来值班，而余数为4，因此从乙往后数到第4个人是甲来值班。

　　3( 单选题 )一块三角地，在三个边上植树，三个边的长度分别为156米、186米、234米，树与树之间的距离均为6米，三个角上都必须栽一棵树，问共需植树多少棵?

　　A. 90棵

　　B. 93棵

　　C. 96棵

　　D. 99棵

　　答案： C， 来源：国家2002

　　考点：植树问题方阵问题

　　解析：因为三角形是一个封闭的图形，且这三条边都能被6整除，所以能够保证三个角均有植树，不用考虑顶点问题。直接套用封闭型植树问题公式：棵树=边长÷间隔=(156+186+234)÷6=576÷6=96棵。因此，本题答案选择C选项。技巧公式法

　　4( 单选题 )有一食品店某天购进了6箱食品，分别装着饼干和面包，重量分别为8，9，16，20，22，27公斤，该店当天只卖出一箱面包，在剩下的5箱中饼干的重量是面包的两倍，则当天食品店购进了( )公斤面包。

　　A. 44

　　B. 45

　　C. 50

　　D. 52

　　答案： D， 来源：国家2007

　　考点：统筹问题

　　解析：在剩下的5箱中饼干的重量是面包的两倍，所以剩下的总重量是3的倍数。注意到：购进的6箱总重量为8+9+16+20+22+27=102公斤，也是3的倍数，因此卖掉的一箱面包的重量也是3的倍数，只可能卖9公斤或27公斤的面包。如果卖掉的一箱面包的重量是9公斤，则剩下的面包为(102-9)÷3=31公斤，剩余的各箱重量无法组合得到31(事实上答案中也没有31+9=40)。如果卖掉的一箱面包的重量是27公斤，则剩下的面包为(102-27)÷3=25公斤，剩余的两箱面包的重量为9公斤和16公斤，总重量为9+16+27=52公斤。因此，本题答案选择D选项。技巧倍数特性法、整体思维法

　　5( 单选题 )如图所示，梯形ABDC的两条对角线AD、BC相交于O，EF平行于两条边且过O点。现已知AB=6，CD=18，问EF的长度为多少?( )

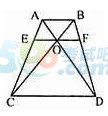
　　A. 8.5

　　B. 9

　　C. 9.5

　　D. 10

　　答案： B， 来源：浙江2008

　　考点：其他平面几何问题

　　解析：AB平行于CD，所以三角型ABO与三角型COD相似。因此AO/OD=AB/CD=6/18=1/3，AO/AD=AO/(AO+OD)=1/4，同理BO/BC=1/4。又△AEO与△ACD相似，因此EO/CD=AO/AD=1/4;同理FO/AB=3/4。因此EF=EO+OF=3/4×AB+1/4×CD=9。

　　因此，本题选择B选项。技巧几何特性法

　　6( 单选题 )2003年8月1日是星期五，那么2005年8月1日是( )。

　　A. 星期一

　　B. 星期二

　　C. 星期三

　　D. 星期四

　　答案： A， 来源：国家2005

　　考点：日期推断类

　　解析： 根据星期日期问题核心口诀：“过一年星期就加一，逢闰日再加一”，从“从2003年8月1日”到“2005年8月1日”一共经过两年，中间经过了一个闰日，所以本题就是在原来星期五的基础上多三天，即为星期一。因此，本题答案选择A选项。因此，本题答案选择A选项。技巧整体思维法

　　7( 单选题 )假设五个相异正整数的平均数是15，中位数是18，则此五个正整数的最大数的最大值可能是( )。

　　A. 24

　　B. 32

　　C. 35

　　D. 40

　　答案： C， 来源：湖南2006

　　考点：构造设定

　　解析：平均数为15，则可求出这五个数之和为15×5=75。若要让其中最大的数尽可能大，则需让其余数尽可能小，由于此五个数为相异的正整数，且其中位数为18，于是可知第一和第二个数最小分别为1和2，第三个数为18，第四个数最小为19，此时，最大的数取得最大值为75-1-2-18-19=35。因此，本题答案为C选项。技巧极端思维

　　8( 单选题 )用八个同样大小的等腰直角三角形拼成一个正方形，若三角形的面积为2平方厘米，那么正方形的周长是( )。

　　A. 8

　　B. 16

　　C. 20

　　D. 32

　　答案： B， 来源：江西2004

　　考点：长度计算

　　解析：三角形的面积是2平方厘米，用这样的三角形8个拼成的正方形面积为2×8=16平方厘米，可知其边长为4厘米，因此周长为4×4=16厘米。因此，本题答案为B选项。

　　9( 单选题 )一间房屋的长、宽、高分别是6米、4米和3米。施工队员在房屋内表面上画一条封闭的线，其所画的线正好在一个平面上且该平面正好将房屋的空间分割为两个形状大小完全相同的部分。问其所画的线可能的最长距离和最短距离之间的差是多少米?

　　A. 6

　　B. 6(√5-1)

　　C. 8

　　D. 4(√13-2)

　　答案： C， 来源：湖北2014

　　考点：长度计算

　　解析：

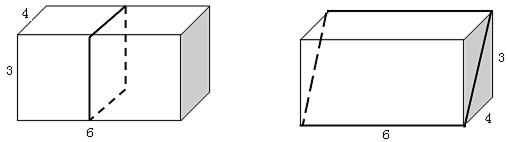
　　几何问题。画图分析容易发现，最短距离为沿着长度为6的棱的中点将长方体(房屋)切成两半，此时所画线的长度为(3+4)×2=14米;最长距离为沿着棱长为3、4的长方形侧面的对角线将长方体切割成两半，此时所画线长度为(6+5)×2=22米。相差为8米。因此，答案选择C项。

　　技巧构造设定法

　　10( 单选题 )100名男女运动员参加乒乓球单打淘汰赛，要产生男、女冠军各一名，则要安排单打赛( )。

　　A. 90场

　　B. 95场

　　C. 98场

　　D. 99场

　　答案： C， 来源：国家2006

　　考点：比赛问题

　　解析：解法一：进行淘汰赛，进行一场比赛，淘汰一支队伍。N个人进行淘汰赛决出男冠军和女冠军，即只有男冠军和女冠军各一名，共两名没有被淘汰。所以就淘汰了98人，就需要98场比赛。因此，本题答案选择C选项。

　　解法二：本题可以进行赋值。假设男运动员有50名，女运动员有50名。根据淘汰赛公式：N支队伍决出冠亚军进行N-1场比赛。男运动员需要打49场，女运动员需要打49场，一共98场。因此，本题答案选择C选项。技巧公式法、赋值法

公务员行测题库【手机题库下载】丨搜索公众微信号"考试吧公务员"

　　相关推荐：

　　2015年国家公务员考试行测数量关系:幂次数列

　　2015年国家公务员考试行测数量关系:积商数列

　　2015国家公务员行测备考化繁为简神秘技巧-整除