2015年公务员行测数量关系热门题型：牛吃草问题

　　一、牛吃草问题基本公式

　　牛吃草问题关键是求出原有草量和草生长的速度或者草枯萎的速度，基本公式为：

　　1.原有草量=(牛吃草的速度-草生长的速度)×吃完的时间

　　2.原有草量=(牛吃草的速度+草枯萎的速度)×吃完的时间

　　对于牛吃草的速度，一般情况下题目不做特别说明，我们就设每头牛每天吃一份草量，然后带入基本公式解题。

　　二、牛吃草问题例题讲解

　　【例1】一片草场上草每天都均匀地生长，如果放牧24头牛，则6天吃完牧草;如果放21头牛，则8天吃完牧草。问如果放牧16头牛，几天可以吃完牧草?

　　A.12 B.14 C.16 D.18

　　【解析】选D。此题为牛吃草问题，由于草是不断生长的，所以相当于追及问题，所以设原有草量为S，每头牛每天吃一份草量，草每天不断生长，速度设为V，t天可以吃完则S=(24-v)×6=(21-v)×8=(16-v)×t可求S=72，v=12，t=18。

　　【例2 】由于天气逐渐变冷，牧场上的草每天以均匀的速度在减少。经计算，牧场上的草可供20头牛吃5天，或供16头牛吃6天。那么可供11头牛吃几天?

　　A.12 B.10 C.8 D.6

　　【解析】选C。设原有草量为S，每头牛每天吃一份草量，草每天匀速枯萎，速度设为V，t天可以吃完，S=(20+v)×5=(16+v)×6=(11+v)×t，解得s=120、v=4、t=8，此题由于草匀速枯萎，同时牛每天要吃草，牛吃的草量与草枯萎的量共同把这片草场的草吃光了，所以相当于一道相遇问题。

　　三、牛吃草问题变形

　　【例3】某矿井发生透水事故，且矿井内每分钟涌出的水量相等，救援人员调来抽水机抽水，如果用两台抽水机抽水预计40分钟可抽完;如果4台同样的抽水机，16分钟可抽完。为赢得救援时间，要在十分钟内抽完矿井内的水，至少需要抽水机()台。

　　A.5 B.6 C.7 D.8

　　【解析】选B。设原有水量为S，每台抽水机每分钟抽水量为1，每分钟出水速度为v，需要N台抽水机，则S=(2-v)×40=(4-v)×16=(N-v)×10，

　　解得

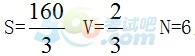
　　在此类排水问题中，一般情况下是排水速度在变化，而进水速度是恒定的，因此这类问题实际上也是牛吃草问题的变形。

　　专家提醒考生，牛吃草问题的变形比较多，在解题过程中要注意哪些量是变化的哪些量是不变的，注意区分哪个是牛吃的速度哪个是草生长或者枯萎的速度，各个量分析清楚了，解题就非常简单了。

关注"考试吧公务员"官方微信第一时间获取公务员报名、真题答案、备考信息!

公务员考试题库【手机题库下载】丨搜索公众微信号"566公务员"

　　相关推荐：

　　2015上海公务员考试行测备考：巧用抽屉原理

　　2015上海公务员考试行测：数学运算之追及问题

　　2015上海公务员考试行测数量关系重点：余数问题