2015年广东公务员考试《行测》追击相遇问题

　　行程问题中的相遇追击问题可以说是公务员考试行测行程问题中的一个母题，很多行程问题中的小题型如牛吃草问题、多次相遇问题、青蛙跳井问题、间隔发车问题、钟表问题等等都是由追击相遇的基本模型展开的，而展开的前提就是时间，就此考试吧为考生梳理一下追击相遇的基本公式：

　　相遇模式：路程和=速度和×时间

　　追击模式：路程差=速度差×时间

　　广大考生朋友要注意的是，这里的追击相遇模式，并不代表真正的追击和相遇，只要是满足时间一定(几个量完成路程所花的时间一定)时，我们知道路程和就可以用相遇模式，知道路程差就是追击模式。

　　(一) 相遇追击模式之钟表问题

　　另：相邻小时刻度间距为30度

　　对于钟表问题而言，我们做题的入手点就是，我们通过判断可以得到路程和还是路程差。知道路程和，就可以用相遇模式解决;知道路程差我们可以用追击模式来解决。通过例题来看一下：

　　现在为北京时间15:00，请问多少分钟后时针与分针第一次重合?

　　这道题的入手点就是判断已知路程和路程差的问题，我们都知道北京时间15:00时分针与时针的间距为90度，题目要求分针与时针第一次重合，所以可以判断这90度就是分针和时针的路程差，所以由15：00变成分针与时针重合用的时间等于90/(6-0.5)。

　　(二)相遇追击模式之牛吃草问题

　　牛吃草问题又称之为牛顿牧场问题或者是消长问题，它的母题也是相遇追击模式。首

　　先我们通过一道例题来认识一下牛吃草问题：

　　一片牧草(牧草每天均匀生长或者均匀枯萎)，可以供7头牛吃8天，可以供12头牛吃5天。请问：

　　(1)如果牧草每天均匀生长可以供9头牛吃几天?

　　(2)如果牧草每天均匀生长，要使牧草永远不被吃光，最多可以养多少头牛?

　　(3)如果牧草每天均匀枯萎可以供9头牛吃几天?

　　这时我们可以发现，如果牧场每天均匀生长，那么这道题目就是一个基本的追击模型，就是牛吃草量—草生长量=原牧草的量。草永远不被吃光就是每天牛吃的量=每天草长的量。如果牧草每天枯萎那么就是一道相遇的模型：牛吃草量+草枯萎量=原牧场的量。

　　所以解决牛吃草问题的关键就是表达出牛每天牛吃的量和草长的量。

　　在这道题目中由于原有牧草量是相同的，也就意味着每天草长的量是相同的，所以我们可以设，一头牛一天吃1份的量，草生长或枯萎x份量，在套入追击或相遇公式：

　　(1)：(7-x)8=(12-x)5=(9-x)T ，求出T即可。

　　(2)：(7-x)8=(12-x)5， 求出x即可。

　　(3)：(7+x)8=(12+x)5=(9+x)T，求出T即可。

　　但是如果原有牧草量不同，或者动物吃草的量不同(如吃草的除了牛还有羊、兔子)该怎么入手呢，记住关键就还是表达出动物每天牛吃的量和草长自己消长的量。例如：

　　牧草每天均匀生长，17头牛，吃光15亩的草需要6天;15头牛，吃光同样的牧草12亩需要4天，求19头牛吃光同样的牧草23亩需要几天?

　　我们发现此时原有牧草量就是不相同的，因此每天草长的量也不相同，所以我们需要将不同草每天长的量表达出来。

　　我们还是设一头牛一天吃一份草，但是草长的量我们设为x份/亩。

　　这道题目的等式变为(17-15x)6=(15-12x)4=(19-23x)T

　　求出T即可。

　　(三)相遇追击模式之多次相遇问题

　　对于任意一道行程问题而言，统一的突破口都在于找不变的量，多次相遇也是一样的。在多次相遇中，我们分为环形上的多次相遇和直线上的多次相遇，但是无论环形上的多次相遇还是直线上的多次相遇，我们都要清楚，速度和不变是解决多次相遇的基本立足点，在速度和不变的基础上我们研究，一次、二次、三次……相遇的时间与路程关系。

　　例题：AB两地相距S，甲乙二人分别从AB两地同时相向而行。甲的速度为S甲，乙的速度为S乙，两人第一次相遇点为C点，时间为T，两人第一次相遇后没有停下，而是继续向对方出发地行驶，到达对方出发地后返回，直到2次相遇、三次相遇……

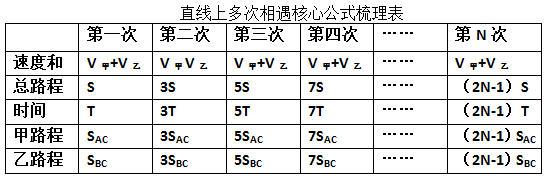
　　在梳理清楚基本公式的基础上相信广大考生对于任意一道多次相遇问题都能够短时间内解决。

　　(四)相遇追击模式之青蛙跳井问题

　　青蛙跳井问题的母题如下：一口井深20米，一青蛙在井的底部往上跳，每次上跳5米下滑2米，问：青蛙跳几次可以跳出此井?

　　对于类似的青蛙跳井问题的解题突破口在于，最后一次青蛙跳上来后是不用下滑的，所以上5米下2米的总路程就变为20-5=15米。

　　前15米，青蛙跳5米滑2米，即每次跳3米。15÷3=5次，加上不用下滑的最后一次共六次可以跳上来。

　　当然这只是一个母题，在行测中会怎么考呢?我们通过一道真题来分析一下：

　　甲乙两人计划从A地步行去B地，乙早上7∶00出发，匀速步行前往，甲因事耽搁，9∶00才出发。为了追上乙，甲决定跑步前进，跑步的速度是乙步行速度的2.5倍，但每跑半小时都需要休息半小时，那么甲什么时候才能追上乙?

　　A. 10∶20 B. 12∶10

　　C. 14∶30 D. 16∶10

　　这道题出现了基本的速度比，V甲：V乙=5:2，所以我们就设甲的速度为5，乙的速度为2。进而他们间的追击距离为2×2=4。这时我们分析甲乙的行进情况甲跑半小时休息半小时，所以每小时的速度差为2.5-2=0.5。同时我们应该清楚，最后追击的半小时甲追上乙以后甲是不用休息的，而最后半小时甲乙的速度差为2.5-1=1.5。所以甲乙实际的追击路程为4-1.5=2.5。此2.5的追击路程用时为2.5÷0.5=5小时，加上最后的0.5小时共计5.5小时，所以甲在14:30时刻追上乙。

关注"考试吧公务员"官方微信第一时间获取公务员报名、真题答案、备考信息!

公务员考试题库【手机题库下载】丨微信搜索"566公务员"

　　相关推荐：

　　2015年广东公务员考试《行测》正确使用成语

　　2015年广东公务员《行测》从基础解排列组合

　　2015年广东公务员《行测》中国地理常识考点