2016北京公务员行测技巧：两招搞定容斥问题

　　容斥问题在公务员考试行测中是很常见的一种题型，难度相对来说也不大，但是有些考生对于容斥问题的理解还不是很清晰，不能很好地解决其中的问题。在此考生吧就将容斥问题的解法做一下总结，希望考生也能够快速掌握，在考场上又快又准地做出容斥相关问题。

　　容斥问题简单来说就是一种计数原理，一般先把所有的情况都相加，再把重复的情况排除掉，这样就能得出计算结果。在行测考试中我们常见的是两者容斥和三者容斥问题。无论是解决两者容斥还是三者容斥，基本的方法有两招：一招是文氏图，这也是很多考生常用的方法;另一招就是用公式。这两招说起来很简单，但是什么情况下用文氏图什么情况下用公式呢?考试吧在此就向大家细细说明。

　　第一招：文氏图

　　我们从简单的两者容斥问题开始看看用文氏图如何解题。

　　例1.某班对50名学生进行体检，有20人近视，12人超重，4人既近视又超重。该班有多少人既不近视又不超重?

　　A.22人 B.24人 C.26人 D.28人

　　解析：根据题目画出文氏图，如下图所示，由题干可知近视和超重的人一共是20+12-4=28人，总人数是50人，那么既不近视又不超重的人有50-28=22人。故答案选A。

　　下面再看看较为复杂的三者容斥问题。

　　例2.某调查公司对甲、乙、丙三部电影的收看情况向125人进行调查，有89人看过甲片，有47人看过乙片，有63人看过丙片，其中有24人三部电影全看过，20人一部电影也没有看过，则只看过其中两部电影的人数是( )。

　　A.69人 B.65人 C.57人 D.46人

　　解析：根据题意画出文氏图，如下图所示。看过甲、乙、丙三部电影的人有：125-20=105人，那么只看过其中两部电影的人数是：(89+47+63)-2×24-105=46人。故答案选D。

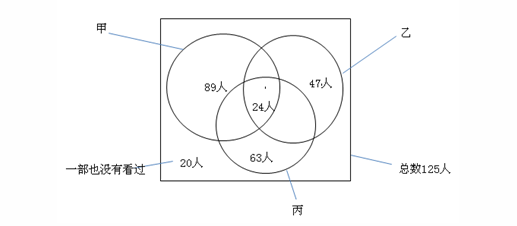
　　通过上面两道题目我们可以体会到当题目中不涉及最大值或最小值时，直接画文氏图就可以解决问题，利用文氏图解决问题的时候只要把全部的情况都算上，再把重复的变为单次的就可以了。

　　第二招：公式

　　例3.在100个学生中，音乐爱好者有56人，体育爱好者有75人，那么既爱好音乐又爱好体育的人最少有多少人?最多有多少人?

　　解析：既爱好音乐又爱好体育的人其实就是下图中两个集合的交集，当一个集合完全融于另一个集合时交集最大。

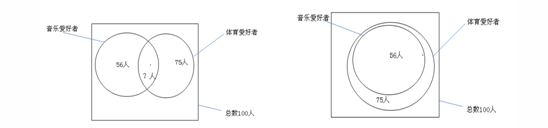
　　也就是说既爱好音乐又爱好体育的人最多有56人。两个集合分别用A、B表示。那么(A∩B)max =min {A，B}。同理三者容斥的最大值(A∩B∩C)max =min {A，B，C}。

　　那么什么时候两个集合的交集最小呢?我们知道：全集=爱好音乐+爱好体育-既爱好音乐又爱好体育+既不爱好音乐也不爱好体育，即I=A+B-A∩B +○，A∩B=A+B+○-I，A、B、I是固定不变的，求A∩B的最小值，那就要求○也最小，○最小可以为0。那么可知(A∩B)min=A+B-I，同理(A∩B∩C)min=A+B+C-2I，(A∩B∩C∩D)min=A+B+C+D-3I。

　　那么在本题中既爱好音乐又爱好体育的人最少有56+75-100=31人。

　　考试吧提醒考生，用以上两招解答容斥问题首先要分清楚题型，求最大值或最小值直接用公式，其余题目画文氏图就可以了，考生们可以通过多练习去体会并加深印象!

关注"566公务员"官方微信，获取最新资讯、职位表、真题答案等信息!

公务员考试题库【手机题库下载】丨微信搜索"566公务员"

　　相关推荐：

　　2016北京公务员申论热点：斩断敲诈删帖产业链

　　2016北京公务员行测：重难点讲解之多次相遇问题

　　2016北京公务员申论技巧：以不变应万变的开头方式