2018行测数学题：几何染色，灰飞烟灭

　　点击查看 更多行测备考指导>>

　　一、立体几何染色问题的基础知识

　　在一个边长为n的正方体表面全部涂上蓝色，将其切成边长为1的小正方体，则在这些小正方体可分为3面有色、2面有色、1面有色和0面有色四种。从下图上我们看出一个正方体有8个顶点，12条棱，6个面，其中顶点上的8个小正方体3面都涂上了蓝色，在棱上而不在顶点上的小立方体2面涂上了蓝色，正方体的外表面非棱非角部分面涂了蓝色。故：

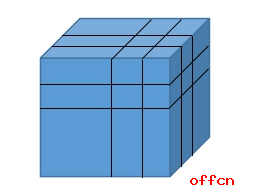
　　3面有色的一共有：8个;

　　2面有色的一共有：12×(n-2)个;

　　1面有色的一共有：6×(n-2)2个;

　　0面有色的一共有：(n-2)3个。

　　同理，我们可以拓展到长方体。在一个长、宽、高分别为a、b、c的长方体表面全部涂上颜色，将其切成边长为1的小正方体，则在这些小正方体可分为3面有色、2面有色、1面有色和0面有色四种，其中：

　　3面有色的一共有：8个;

　　2面有色的一共有：4×{(a-2)+(b-2)+(c-2)}个;

　　1面有色的一共有：2×{(a-2)×(b-2)+(a-2)×(c-2)+(b-2)×(c-2)}个;

　　0面有色的一共有：(a-2)×(b-2)×(c-2)个。

　　二、真题应用

　　1、一个边长为8cm的立方体，表面涂满油漆，现在将它切割成边长为0.5cm的小立方体，问两个表面有油漆的小立方体有多少个?

　　A、144 B、168 C、192 D、256

　　【中公解析】两个表面被涂油漆的小立方体在棱上而不在顶点上。大立方体棱长为8cm，切成小立方体棱长为0.5cm，则每条棱被分成16段，其中两端不符合要求，因此每条棱上有14个小立方体符合。立方体共有12条棱，则符合要求的小立方体有14×12=168个。故正确答案为B。

　　2、将一个8厘米×8厘米×1厘米的白色长方体木块的外表面涂上黑色颜料，然后将其切成64个棱长1厘米的小正方体，再用这些小正方体堆成棱长4厘米的大正方体，且使黑色的面向外露的面积要尽量大，问大正方体的表面上有多少平方厘米是黑色的( )。

　　A、84 B、88 C、92 D、96

　　【中公解析】由长方体木块切得的小正方体中，4面黑的只有4块，2面黑的正方体有24块，而大正方体2面黑的刚好需要24块，用完，3面黑的需要8块，现在只有4块，少了4，则只能用1面黑的代替，所以每个都少了2个面，共4个，则少8个面，少了8平方厘米，故大正方体表面黑色的面积为：4×4×6-8=88。故正确答案选B。

　　3、一个5×5×5的立方体表面全部涂上红色，再将其分割成1×1×1的小立方体，取出全部至少有一个面是红色的小立方体，组成表面全部是红色的长方体，可组成的长方体的体积最大是：

　　A、125 B、98 C、96 D、94

　　【中公解析】至少有一个面是红色的小立方体一共有：53-(5-2)3=125-27=98个，8个3面涂色的在长方体8个顶点处，(5-2)×12=36个2面涂色的在长方体的12条棱上，一面涂色的98-8-36=54个只能放在面的中间和里面。当新长方体体积为98时，其长、宽、高分别为7、2、7(98=2×7×7)，2面涂色的需要(7-2)×8=40个，40>35，不满足，故排除B;当新长方体体积为96时，其长、宽、高分别为6、4、4(96=4×4×6)，2面涂色的需要(4-2)×8+(6-2)×4=32个，32<35，满足要求，所以可组成的长方体的体积最大是96。故正确答案选C。

扫描/长按二维码可帮助公考通关

获取精选2018模拟试题

下载2018年公考职位表

获取2018公考通关技巧

获取历年公考真题试卷

公务员万题库下载｜ 微信搜"万题库公务员考试"

　　相关推荐：

　　2018年公务员考试国内外时事政治热点汇总

　　干货！你关心的民生大事，政府工作报告都提到了

　　公务员行测综合指导 | 行测言语理解 | 行测数量关系

　　公务员行测判断推理 | 行测常识判断 | 行测资料分析

　　2018公务员申论热点 | 申论范文 | 申论指导 | 经验技巧

　　2018年公务员考试答案 | 2018年公务员考试真题答案