2019国考行测技巧：数量关系之巧解利润问题

　　利润问题为数量关系考试中考察较为频繁的一类问题，在青海省考及事业单位考试当中经常会出现，因此熟练掌握利润问题的相关概念公式及解题方法对于开始较为重要，本文将全面介绍利润问题相关公式及解题方法，考试吧希望考生学习之后对于利润问题有所了解和掌握!

　　一、概念及公式

　　利润问题所涉及的概念包括：成本(进价)、定价、售价、利润、利润率、打折率、折扣对于理解这些概念可通过下面的小例子：

　　张三在旅游期间准备贩卖旅游纪念品，已知开始时张三进了一件纪念品100元(成本)，第二天想用200元的价格(定价)出售，结果一周内无人愿意购买，最终张三采取策略，在原价基础上打9折出售(打折率90%)，最终以180元出售(售价)，获得80元钱(利润)，最终获利80%(利润率)

　　小结：上述例子当中需要做重点强调的就在于：1、数量关系考试中成本等于进价，两种表述形式相同，2、利润率为获利的百分数，表述形式一般为获利或者盈利百分之多少。对于概念间常用公式如下：1、利润=售价-成本2、打折率=售价÷定价3、利润率=利润÷成本4、售价=成本×(1+利润率)5、成本=售价÷(1+利润率)以上所述公式均为重点考察的内容，尤其是利润率公式我们也可以额看出利润是以成本为基础，例如获利70%是获得成本的70%的利润。

　　例1：某汽车销售中心以每辆30万的价格出售了两辆小汽车，一辆获利50%，一辆亏损40%，则该汽车销售中心的盈亏额为?

　　A赚10万 B亏10万 C赚20万 D亏20万

　　解析：由公式成本=售价÷(1+利润率)得到第一辆汽车成本为30÷(1+50%)=20第二辆汽车成本=30÷(1-40%)等于50万，则总成本70万，售价卖60万，亏10万，答案选B。

　　二、解题方法

　　方法1：方程

　　应用环境：题干中存在较多的实际值并且存在等量关系

　　例2：某书店出售一种类图书，每出售一本可获利18元，按原价出售总数的40%后，每本减价10元，直至全部售完，共获利3000元，那么，该书店共售出这种图书多少本?

　　A250 B300 C350 D400

　　题目关键：18元、10元、3000元均为实际值，且共获利3000元体现了明显的等量关系两波图书利润和等于3000元

　　解析：设总数为X本则可得方程：40%X×18+60%X×8=3000，得X=250本

　　方法2：特值

　　应用环境：所求问题为比值关系且对应量均未知

　　例3：某商品按原价出售，每件商品可获得50%利润，后来按照原价的80%出售，结果每天售出的件数比降价前增加了2倍，那么后来每天销售这种商品所赚取的利润是原来的多少倍?

　　A0.8 B1.2 C1.5 D1.8

　　题目关键：所求结果为倍数为一个比值问题且对应的前后利润额未知

　　利润问题存在比较时解题小技巧：列表

　　解析：　　

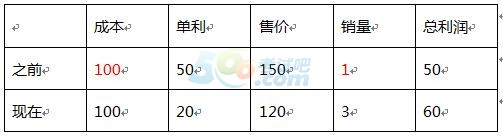
　　表格中标红之处为所设的特值，围绕所设特值尽可能整及尽可能小的原则可将商品成本设为100，之前销量设为1，其他变量可根据题干信息进行逻辑推导最终可知总利润前后为1.2倍

　　方法3：方程+特值

　　例4：一种商品今年的成本比去年下降了10%，但是售价没变，因此利润上升了20%，则这种商品今年的售价是成本几倍?

　　A、4∕3 B、5∕3 C、5∕4 D、7∕3

　　题目关键：所求为倍数是一个比值关系

　　售价未变存在等量关系

　　解析：　　

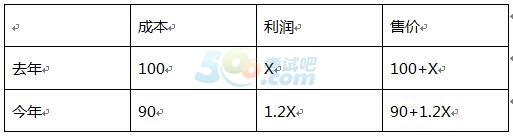
　　根据等量关系售价未变，可得100+X=90+1.2X，则X=50，因此今年的售价为150元

　　所求倍数为150∕90即5∕3

　　利润问题难度适中，适合在考场中选用针对性的方法进行解决，当然利润问题解题方法还包括十字交叉法，因为十字交叉法能解决的问题都可以用特值进行计算，因此在本文中就不再提及十字交叉法解决利润问题的内容，希望通过本文考生能够熟练利润问题的相关概念、公式以及解题方法。

扫描/长按二维码可帮助公考通关

获取2018公考成绩查询

下载2018年公考分数线

获取公务员面试公告

获取历年公考真题试卷

公务员万题库下载｜ 微信搜"万题库公务员考试"

　　相关推荐：

　　2019国考行测技巧：五大模块时间分配

　　2019国考行测技巧：人文知识考点

　　2019国考行测技巧：从细节防陷阱

　　2019国考行测技巧：资料分析备考指南

　　2019国考行测技巧：文字型材料阅读技巧

　　2019国考行测技巧：工程问题解题技巧汇总

　　2018年国家公务员考试《申论》备考指导汇总

　　2018年国家公务员考试《行测》备考指导汇总