2019公务员行测技巧：巧用隔板法破解排列组合难题

　　如果让你把7个大小相同的橘子分给4个小朋友，要求每个小朋友至少分到1个橘子，问一共有多少种不同的分法?

　　看完问题后，你能快速得出答案吗?如果难倒你的话，那就说明你对排列组合中的隔板法还不太了解哦!这种题型在公考中出现的概率很大，不会的小伙伴不妨先和小编一起来学习一下吧。(解锁正确分法下拉至文末)　　

　　首先，让我们一起来正确认识一下隔板法

　　隔板法主要针对的是相同元素的不同分堆问题。我们也可以把它理解为：

　　如果把n个相同的元素分给m个不同的对象，每个对象至少有一个，问有多少种不同的分法的问题。其基本公式为：

　　然后，再来看一下隔板法都有哪些题型特征

　　隔板法一共有三种题型：①标准型、②多分型、③少分型，后两种都需要基于“标准型”来解题，具体要怎么操作呢?别急，我们先通过一个经典真题来检测一下大家对于隔板法的掌握程度。

　　【经典真题】某单位共有10个进修的名额分到下属科室，每个科室至少1个名额，若有36种不同分配方案，则该单位最多有多少个科室?

　　A.7 B.8 C.9 D.10

　　【解析】正确答案为B。

　　下面我们再来通过3个例题分别介绍一下隔板法的三种题型特征及应用，接着往下看

　　1、标准型：

　　标准型需要同时具备的3个要求：(1)被分配的n个元素无差别;(2)这n个元素分给m个不同对象;(3)每个对象至少分一个元素。　　

　　【解析】正确答案为C。

　　【解题思路】本题中相同的元素是6本相同的书，故n=6;放进4个抽屉，即将书分成4堆，故m=4;每个抽屉至少放1本书，故本题为隔板法中的标准题型。

　　【解题方法】把6本书排成一排，因为书是相同的，不存在排列顺序问题。要把这6本书分成4堆，只要在这6本书形成的空隙中插入5个隔板即可。6本书排成一排，形成了7个空。但是，因为要求每个抽屉至少放1本书，所以最前面的空和最后一个空是不能插板的，则只能在中间形成的5个空中插入3个隔板，即从5个空中选择3个空插入隔板，代入公式：　　

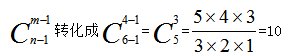
　　2、多分型

　　多分型需要同时具备的3个要求：(1)被分配的n个元素无差别;(2)这n个元素分给m个不同的对象;(3)每个对象至少分x个元素。　　

　　【解析】正确答案为D。

　　【解题思路】此题中没有要求至少发1份，而是要求至少发9份的，因此需要将其转化为标准型的隔板模型，方法就是先每个部门分x-1个元素，剩下的元素就转化为每个部门至少分一个元素了。

　　【解题方法】假设三个部门分别为A、B、C，每个部门可以先分8份，然后再把剩下的6份发给3个部门，保证每个部门发1份，代入公式：　　

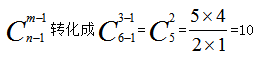
　　3、少分型

　　少分型需要同时具备的3个要求：(1)被分配的n个元素无差别;(2)这n个元素被分给m个不同的对象;(3)被任意分给这m个不同的对象。　　

　　【解析】正确答案为B。

　　【解题思路】这道题中说每个盒子可以为空，就意味着有的盒子可以分0个元素，因此可以采用“先借后还”的思路，先向每一个盒子借一个元素，总共就会有n个元素了，由于借了一个元素，接下来在分的时候，每个盒子则至少需要分一个，这样就转化成了标准的隔板模型。

　　【解题方法】在分之前先向每个盒子借3个小球，总共就会有23个小球，接下来分的时候需要再给每个盒子一个小球，就变成每个盒子至少分一个小球了，有多少种分法，代入公式：　　

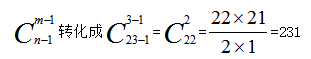
　　以上就是今天所讲的排列组合之隔板法的运用了，希望大家理解并能熟练运用，为行测得高分奠定坚实的基础!

　　【上文解锁】一共有20种不同的分法，你做对了吗?

　　【解析】此题为隔板法的标准型，因为相同的元素是7个大小相同的橘子，故n=7;给4个小朋友，故m=4;所以只要在这7个橘子之间插入6个隔板即可，代入公式：　　

扫描/长按二维码获取国考分数线

获取2019年国考分数线

获取2019国考成绩查询

获取2019国考面试指导

获取历年公考真题试卷

公务员万题库下载｜ 微信搜"万题库公务员考试"

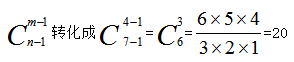
　　相关推荐：

　　2019国考行测技巧：如何提升做题速度