2020公务员行测数量关系备考：带你玩转年龄问题

　　在行测考试中，年龄问题是一类以“年龄为内容”的数学应用题。那到底应该如何在公务员考试过程中快速解答年龄问题呢?接下来考试吧公务员考试网带大家分析一下。

　　年龄问题的主要特点(也是题中的隐藏条件)两个人之间的年龄差是保持不变的，它不随岁月的流逝而改变;两个人各自的年龄随着岁月的变化，将增加或减少同一个自然数;两个人之间年龄的倍数关系会随着年龄的增长而发生变化，年龄增大，倍数变小。

　　【解析】

　　根据题目中的条件，我们经常会把年龄问题化为“和差问题”、“和倍问题”、“差倍问题”进行求解。

　　解题训练

　　例题1：儿子今年10岁，5年前母亲的年龄是他的6倍，母亲今年多少岁?

　　【解析】

　　根据题中所给的条件，为了方便计算，我们把儿子5年前的年龄设为x，则母亲5年前的年龄就是6x，最后可以形成这样一个表格(如下表)，但我们怎样利用这个表格解出我们需要的答案呢?我们不要忘了年龄问题的主要特点，也就是题中的隐含条件：儿子和母亲今年与5年前的年龄都相差5岁。　　

　　儿子今年是10岁，根据隐含条件，那5年前儿子的年龄就应该是5岁，即x=5，则6x=30，也就是母亲5年前的年龄是30岁，那么母亲今年的年龄就是30+5=35岁。

　　通过这道题，我们知道了表格以及题中的隐含条件如何去用，其实对于这道题我们不用写表格，直接分析也可以分析出来，那是因为这道题相对比较简单，没有很好的体现出来使用表格的优越性，如果换做一道比较复杂的年龄问题，用表格去分析就非常清晰了。

　　例题2：张爷爷有一个儿子和一个孙子，祖孙三代现在的年龄和为103岁，且张爷爷儿子的年龄是孙子年龄的6倍，当张爷爷的年龄是儿子现在的年龄时，儿子的年龄比现在孙子的年龄大5岁，问当孙子长到儿子现在的年龄时，张爷爷的年龄是多少岁?

　　【解析】

　　题中说张爷爷儿子现在的年龄是孙子现在年龄的6倍，所以为了方便计算我们把孙子现在的年龄设为x，则儿子现在的年龄就是6x，由于祖孙三代现在的年龄和为103岁，所以爷爷现在的年龄是103-6x-x=(103-7x)岁;当张爷爷的年龄是儿子现在的年龄时，也就是张爷爷的年龄为6x时，儿子的年龄比现在孙子的年龄大5岁，由于孙子现在的年龄是x，所以当张爷爷的年龄为6x时，儿子的年龄为x+5;最后问题问的是当孙子长到儿子现在的年龄时，也就是孙子的年龄是6x时，爷爷多少岁?

　　通过对题目中已知条件的分析，我们可以得到下面这个表格：　　

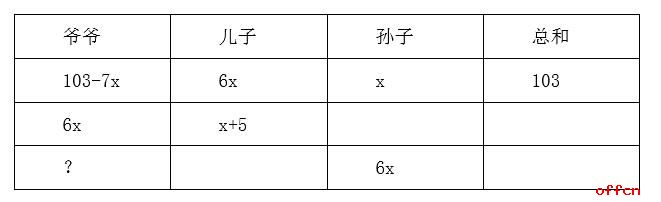
　　所以现在我们要想求出最终的结果就需要把x的值求出来，这时候我们就需要在表格当中找出存在的等量关系，解出x值。那我们怎么找等量关系呢?这个时候我们就要用到年龄问题的第一个特点了：两个人之间的年龄差是保持不变的，通过我们观察表格中的已知数据，我们可以得到爷爷和儿子两个人在不同阶段的年龄差，所以利用年龄差相等，就可以列出等式：103-7x-6x = 6x-(x+5)，解出x=6，则，6x=36,103-7x=61，也就是说当孙子的年龄是6岁时，爷爷的年龄是61岁;那当孙子的年龄是36岁时，根据两人年龄差是保持不变的这个特点，爷爷的年龄就应该是61+(36-6)=91岁。

　　通过这两道题我们会发现，如果我们在分析年龄问题的过程中，用表格的方式呈现出来，在做比较复杂的题时就会很清晰很容易的找出等量关系求出x值，从而得到我们要求的结果，这就是考试吧公务员考试网为大家讲解的表格的优势，希望大家能够早日上岸。

扫描/长按二维码可帮助公考通关

获取2020公考报名时间

获取2020年公考职位表

获取2020公考最新资讯

获取历年公考真题试卷

公务员万题库下载｜ 微信搜"万题库公务员考试"

　　相关推荐：

　　2020国考行测常识备考：历史易错点总结

　　2020国考行测资料分析中有关倍数的小技巧

　　2020国考行测判断推理备考：图形推理中折叠问题

　　2020国考行测常识判断重要考点：监察法知识点

　　2020国考行测重要考点解读：多次相遇问题

　　2019公务员国内外时事政治热点∣2020报名时间