2020国家公务员考试行测技巧：多次相遇题型总结

　　行程问题几乎是近几年行测数量运算考试的必考题型，而多次相遇是行程问题中的其中一个考点，考试几率相对较大，广大考生觉得这个题型是个难点，但其实掌握题型规律和方法，很容易拿到分数。所以弄清楚命题规律显得尤为重要，下面跟着考试吧公务员考试网一起来看看多次相遇常见题型。

　　一、多次相遇运用理论(直线异地多次相遇)　　

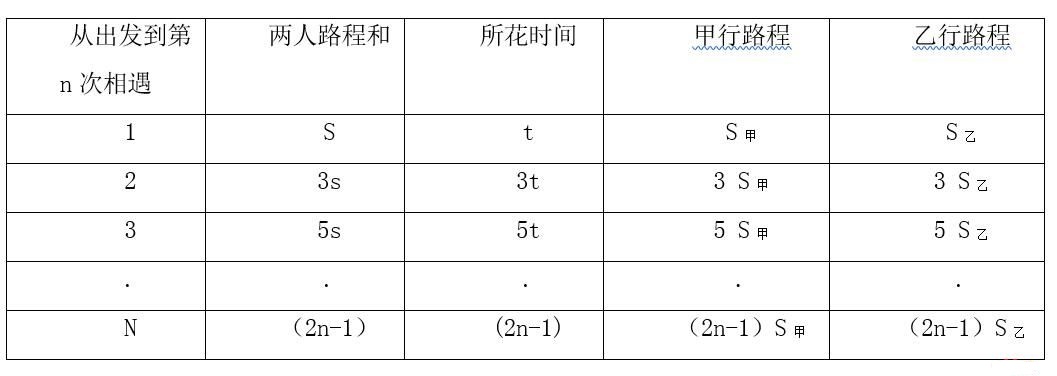
　　二、多次相遇常见题型

　　1、求路程

　　例题1.

　　A大学的小李和B大学的小孙分别从自己学校同时出发，不断往返于A、B两校之间。现已知小李的速度为85米/分钟，小孙的速度为105米分钟，且经过12分钟后两人第二次相遇。问A、B两校相距多少米?

　　A.740 B.750 C.760 D.770

　　【答案】C。

　　解析：已知经过12分钟多次相遇，则第一次相遇时间为12÷3=4，AB两地相距距离即为两人第一次相遇距离(85+105)×4=760千米。

　　例题2.

　　甲、 乙两军分别同时从A、B两地相对开出，第一次在离A地95千米处相遇。相遇后继续前进到达对方出发点后又立刻返回,第二次在离B地25千米处相遇。求A、B两地间的距离是多少千米?

　　A.260 B.285 C.310 D.325

　　【答案】A。

　　解析：第一次在离A地95千米处相遇，即第一次相遇甲走了95千米，则从出发到第二次相遇甲走了95×3=285千米，第二次相遇距离B地25千米，甲第二次走的相比AB的距离多25千米，则AB距离为285-25=260千米。

　　2.求时间

　　例：某高校两校区相距2760米，甲、乙两同学从各自校区同时出发到对方校区，甲的速度为70米/分钟,乙的速度为110米/分钟，在路上二人第一次相遇后继续行进，到达对方校区后马上回返，那么两人从出发到第二次相遇需用多少分钟?

　　A.32 B.46 C.61 D.64

　　【答案】B。

　　解析：已知第一次相遇的时间为2760÷(70+110)，出发到第二次相遇时间为第一次的3倍，即2760÷(70+110)×3=46分钟。

　　3.求相遇次数

　　例.在一次航海模型展示活动中甲乙两款模型在长100米的水池两边同时开始相向匀速航行，甲款模型航行100米要72秒,乙款模型航行100米要60秒。若调头转身时间略去不计，在12分钟内甲乙两款模型相遇次数是:

　　A.9次 B.10次 C.11次 D.12次

　　【答案】C。

　　解析：本题是典型的直线多次相遇问题。由题意可知,第一次相遇所用时间为100÷(100÷72+100÷60)=360/11秒。根据直线多次相遇问题的基本结论:第n次相遇所用时间为第一次相遇所用时间的2n-1倍。本题中,第n次相遇所用时间为360/11(2n-1). 12分钟=720秒= 360/11x22秒,令2n-1≤22,可知n最大可取到11.即在12分钟内可相遇。

　　以上就是考试吧公务员考试网介绍的多次相遇常考题型，了解题型和基本知识点，多加练习培养做题敏感度，拿到这类题的分数其实很容易。

扫描/长按二维码可帮助公考通关

获取2020国考报名时间

获取2020年国考职位表

获取2020国考最新资讯

获取历年公考真题试卷

公务员万题库下载｜ 微信搜"万题库公务员考试"

　　相关推荐：

　　2020国家公务员考试行测主旨观点题解题技巧

　　2020国家公务员考试行测逻辑填空技巧之词语辨析

　　2020国考行测资料分析备考：A×B型式的增长率

　　2020国家公务员考试行测定义判断中的原理效应

　　2020国家公务员考试行测图形推理字母题型怎么解

　　2020国考行测常识备考：那些你需要了解的政治理论

　　2020国家公务员考试行测技巧：多次相遇 简单解决

　　2019公务员国内外时事政治热点∣2020报名时间