文章责编：zhangguojuan
看了本文的网友还看了学历| 高考 中考 考研 自考 成考 外语| 四六级 职称英语 商务英语 公共英语 资格| 公务员 报关员 银行 证券 司法 导游 教师 计算机| 等考 软考
工程|一建 二建 造价师 监理师 咨询师 安全师 结构师 估价师 造价员 会计| 会计证 会计职称 注会 经济师 税务师 医学| 卫生资格 医师 药师 [更多]
| 第 1 页：数量关系 |
| 第 3 页：资料分析 |
| 第 5 页：判断推理 |
| 第 7 页：言语理解 |
数量关系部分
必考点一：公式解决容斥极值
公式：A+B-I=A、B 重叠部分最小值;A+B+C-2I=A、B、C 重叠部分最小值
例：某数学竞赛共160 人进入决赛，决赛共4题，做对第一题的有136 人，做对第二题的有125 人，做对第三题的有118 人，做对第四题的有104人。那么，在这次决赛中至少有几人得满分?
A. 3 B. 4 C. 5 D. 6
【答案】A。
【解析】根据公式，即136+125+118+104-3×160=3人。
必考点二：合作完工问题考查效率比方法：
给时间，有效率比，求总量的比较时，可直接设出效率值方便解题
例：甲乙丙完成同一项工程的时间比是20∶15∶12，甲队单独完成A 工程需要60 天，丙队单独完成B 工程需要70 天，现丙队负责A 工程，甲乙两队共同负责B工程，则A，B两工程的完成情况为( )。
A. A工程比B工程提前14 天
B. B 工程比A工程提前14 天
C. A工程比B工程提前16 天
D. B 工程比A工程提前16 天
【答案】A。
【解析】由题意知甲乙丙效率之比是3∶4∶5，设甲乙丙工作效率分别为3、4、5，则A工程量是60×3=180，B工程量为5×70=350，甲乙完成B所用的天数是350÷7=50，丙完成A 所用的天数是180÷5=36，则完成A工程比完成B工程快了14天。
必考点三：正难则反的排列组合
方法：问题中有“至少”，往往正面考虑繁琐，反面考虑简单
例：某工厂从10个不同的样品零件中抽出3 个做检验，已知这10个零件中有3 个是不合格的，则抽出零件中至少有一个是不合格的取法有多少种情况?( )
A. 70 B. 85 C. 375 D. 510
【答案】B。
必考点四：等积转化求阴影面积
方法：同底(高)等高(底);全等
例：平行四边形ABCD，E、F 分别是AB、CD 上的点，AF 与DE交于P点，BF 与CE 交于Q 点，已知△ADP 的面积为20，△BCQ 的面积为30，求图中阴影部分的面积。
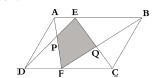
A. 25 B. 35 C. 40 D. 50
【答案】D。
【解析】连接EF，由△ADF 与△EDF 同底等高，则面积相等，故△ADP与△EFP面积相等，△EFP 面积为20。同理，△EFQ面积为30。所求阴影面积为50。
必考点五：和定求最小值的最小值
方法：求极小值时，则令其余量尽可能大
例:某社区共6 人参加跳绳比赛，平均每人跳了126 下，且跳得最多的人比跳的最少的人多跳了74 下，如果每个人跳的数量均不相等，问跳得最少的人最少跳了多少下?( )
A. 63 B. 64 C. 65 D. 66
【答案】D。
【解析】设跳得最少的人跳了x 下，则跳的最多的人跳了x+74下。则(x+74)+(x+73)+(x+72)+(x+71)+(x+70)+x=6×126，解得x=66。
必考点六：直线多次相遇看倍数
方法：两人同时相向出发并不停地在两地间往返，第n 次相遇时两人(单人)走的总路程是两人(单人)第一次相遇时走的总路程的(2n-1)倍
例：甲从A地、乙从B 地同时以均匀的速度相向而行，第一次相遇离A 地6 千米，继续前进，到达对方起点后立即返回，在离B 地3 千米处第二次相遇，则A、B 两地相距多少千米?( )
A. 10 B. 12 C. 18 D. 15
【答案】D。
【解析】第一次相遇甲走了6 千米，第二次相遇时甲共走了6×3=18千米，总路程为18-3=15 千米。
相关推荐：
