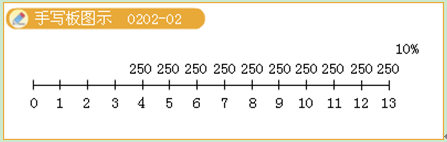
【2003年第一大题第25小题】已知(F/A，10%，9)=13.579，(F/A，10%，11)=18.531。则10年，10%的即付年金终值系数为(　)。

　　A.17.531

　　B.15.937

　　C.14.579

　　D.12.579

　　『正确答案』A

　　『答案解析』即付年金终值FA=A[(F/A, i, n+1)-1]

　　则10年，10%的即付年金终值系数=(F/A，10%，11)-1=17.531。

　　【2004年第一大题第1小题】根据资金时间价值理论，在普通年金现值系数的基础上，期数减1、系数加1的计算结果，应当等于(　)。

　　A.递延年金现值系数

　　B.后付年金现值系数

　　C.即付年金现值系数

　　D.永续年金现值系数

　　『正确答案』C

　　『答案解析』即付年金现值PA =A×(P/A,i,n)(1+i)

　　=A×[(P/A,i,n-1)+1]，因此本题的正确答案为C。

　　(3)递延年金现值

　　递延年金的计算方法有三种：

　　计算方法一：先将递延年金视为n期普通年金，求出在递延期期末的普通年金现值，然后再折算到现在，即第0期价值：

　　PA=A×(P/A，i，n)×(P/F，i，m)= 30×(P/A，10%，4)×(P/F，10%，2)

　　式中，m为递延期，n为连续收支期数，即年金期。

　　计算方法二：先计算m+n期年金现值，再减去m期年金现值：

　　PA=A×[(P/A，i，m+n)-(P/A，i，m)]= 30×[(P/A，10%，6)-(P/A，10%，2)]

　　计算方法三：先求递延年金终值再折现为现值：

　　PA=A×(F/A，i，n)×(P/F，i，m+n)= 30×(F/A，10%，4)×(P/F，10%，6)

　　【例2-9】某企业向银行借入一笔款项，银行贷款的年利率为10%，每年复利一次。银行规定前10年不用还本付息，但从第11年至第20年每年年末偿还本息5 000元。要求：用两种方法计算这笔款项的现值。

　　『正确答案』方法一：PA= A×(P/A，10%，10) ×(P/F，10%，10)

　　=5 000×6.1446×0.3855

　　≈11 843.72(元)

　　方法二：PA= A×[(P/A，10%，20)- (P/A，10%，10)]

　　=5 000×(8.5136-6.1446)

　　=11 845(元)

　　两种计算方法相差1.28元，是因货币时间价值系数的小数点位数保留造成的。后面的例题中也有类似的情况，不再一一说明。

　　【例2-10】某公司拟购置一处房产，房主提出两种付款方案：

　　(1)从现在起，每年年初支付200万元，连续付10次，共2000万元。

　　(2)从第5年开始，每年年初支付250万元，连续支付10次，共2500万元。

　　假设该公司的资本成本率(即最低报酬率)为10%，你认为该公司应选择哪个方案?

　　『正确答案』(1)PA= 200×[(P/A，10%，9)+1]

　　= 200×6.7590

　　=1351.80(万元)

　　(2)PA= 250×[(P/A，10%，9)+1]×(P/F，10%，4)=1154.10(万元)

　　或者：PA=250×{[(P/A，10%，13)+1]- (P/A，10%，3)+1}=1154.13(万元)

　　或者：PA=250×[(F/A，10%，11)-1]×(P/F，10%，14)=1153.98(万元)

　　最好为：P= 250×(P/A，10%，10)×(P/F，10%，3)

　　或者：P=250×[(P/A，10%，13)-(P/A，10%，3)]

　　或者：P= 250×(F/A，10%，10)×(P/F，10%，13)

　　由于第二方案的现值小于第一方案，因此该公司应选择第二种方案。

　　(4)永续年金的现值

　　PA (n→∞) =A/i

　　【例2-11】归国华侨吴先生想支持家乡建设，特地在祖籍所在县设立奖学金。奖学金每年发放一次，奖励每年高考的文理科状元各10 000元。奖学金的基金保存在中国银行该县支行。银行一年的定期存款利率为2%。问吴先生要投资多少钱作为奖励基金?

　　由于每年都要拿出20 000元，因此奖学金的性质是一项永续年金，其现值应为：

　　PA =20 000/2%=1 000 000(元)

　　也就是说，吴先生要存入1 000 000元作为基金，才能保证这一奖学金的成功运行。