五、综合题(本类题共2题,共25分,第1小题10分,第2小题15分。凡要求计算的题目,除题中特别加以标明的以外,均需列出计算过程;计算结果出现小数的,除题中特别要求以外,均保留小数点后两位小数;计算结果有单位的,必须予以标明。凡要求说明理由的内容,必须有相应的文字阐述。要求用钢笔或圆珠笔在答题纸中的指定位置答题,否则按无效答题处理。)
50
假设资本资产定价模型成立.表中的数字和字母A—K所表示的数字相互关联。

甲投资者以200万元购入股票1;乙投资者以200万元购入股票2:丙投资者以200万元购入股票3;丁投资者预计如果分别以100万元购入股票1和股票2组成投资组合,则可实现年均16%的收益率。
要求:
(1)计算表中字母A—K所表示的数字(应列出必要的计算过程或理由)。
(2)上述甲、乙、丙投资者的不同投资行为表明他在决策时所预计的股票1、股票2和股票
3的期望收益率分别处于什么水平?
(3)计算丁的投资组合的卢系数和必要收益率,并据以判断丁投资者愿否进行上述投资。
参考解析:
(1)①无风险证券的收益率固定不变,不因市场组合收益率的变化而变化,故无风险证券收益率的标准差为0、无风险证券与市场组合收益率的相关系数为0,无风险证券卢系数为0。即:A=0;B=0;C=0。②根据相关系数和β系数的定义可知,市场组合收益率与自身的相关系数、β值均为1。即:E=1;F=1。
③根据资本资产定价模型的基本表达式,利用股票1和股票2的数据联立成方程组,可求出无风险收益率D和市场组合的必要收益率G:10%=D+0.5×(G-D);25%=D+2×(G-D)解得,D=5%,G=15%。
④根据资本资产定价模型的基本表达式,利用股票3的数据,可求出股票3的β系数K:
30%=5%+K×(15%-5%)解得:K=2.5。
⑤根据β值的计算公式
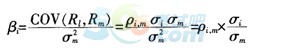
下列各等式成立:
0.5=H×16%/8%=H×2,解得,H=0.25;2=0.8×I/8%=10×I,解得,I=20%;2.5=0.5×J/8%,解得:J=40%。
(2)只有期望收益率不低于必要收益率时,投资者才愿意投资,故上述投资行为表明:甲投资者在决策时预计股票1的期望收益率不低于10%,但股票2的期望收益率低于25%,股票3的期望收益率低于30%;乙投资者在决策时预计股票2的期望收益率不低于25%,但股票1的期望收益率低于10%,股票3的期望收益率低于30%;丙投资者在决策时预计股票3的期望收益率不低于30%,但股票1的期望收益率低于10%,股票2的期望收益率低于25%。
(3)丁投资组合的p系数=0.5×100/(100+100)+2×100/(100+100)=1.25,丁投资组合的必要收益率=5%+1.25×(15%-5%)=17.5%,或丁投资组合的必要收益率=10%×100/(100+100)+25%×100/(100+100)=17.5%,由于丁投资
组合的期望收益率小于必要收益率,故丁投资者不愿投资。
 关注566会计职称微信第一时间获取试题、内部资料等信息!
关注566会计职称微信第一时间获取试题、内部资料等信息!
会计职称题库【手机题库下载】 | 微信搜索"566会计职称"
| 初级QQ群: | 中级QQ群: |
|---|
相关推荐:
·2019会计职称考试《中级经济法》练习题汇总 (2018-11-06 7:06:22)
·2019中级会计职称考试《财务管理》练习题汇总 (2018-11-06 7:03:19)
·2019会计职称《财务管理》练习题:利润最大化 (2018-11-06 10:03:19)
·2019会计职称《财务管理》练习题:企业功能 (2018-11-06 10:01:19)
·2019会计职称《财务管理》练习题:利益冲突与协调 (2018-11-06 10:00:19)
实用文档 | 入党资料 | 入党申请书 | 入党志愿书 | 个人自传 | 转正申请书 | 思想汇报 | 个人简历 | 简历模板 | 简历封面 | 工作计划 | 工作总结 | 自我评测
个性评测 | 社交评测 | 事业评测 | 运势评测 | 报告 | 实习报告 | 工作总结 | 社会实践 | 心得体会 | 述职报告 | 调查报告 | 辞职报告
法律文书 | 合同范本 | 演讲范文 | 更多>>
英语学习 | 听力口语 | 阅读写作 | 翻译文化 | 趣味英语 | 学习方法 | 英文经典歌曲 | 每日课堂 | 空中英语 | 少儿英语 | 影视英语 | 英文歌曲 | 更多>>
作文大全 | 作文 | 小学 | 初中 | 高中 | 话题作文 | 考研 | 四六级 趣味作文 | 体裁作文 | 记叙文 | 议论文 说明文 | 应用文 | 读后感 | 作文素材 | 名言警句
优美段落 | 哲理故事 | 诗词赏析 | 成语知识 | 技巧 | 写作指导 | 作文点评 | 佳文赏析 | 写作基础 | 话题演练 | 作文教学 | 更多>>









