一、选择题(本题共 30 分,每小题 3 分)
1.春节假期,北京市推出了庙会休闲娱乐、传统文化展演、游园赏景赏花、冰雪项目体验等精品文化活动,共接待旅游总人数 9 608 000 人次,将 9 608 000 用科学记数法表示为
(A) 9608 ´103 (B) 960.8 ´104
(C) 96.08 ´105
(D) 9.608 ´106
2.在数轴上,实数 a,b 对应的点的位置如图所示,且这两个点关于原点对称,下列结论中,正确的是( )
(A) a + b = 0
(B) a - b = 0
(C) a < b
(D) ab>0
3.如图,AB∥CD,DA⊥CE 于点 A.若∠EAB=55°,则∠D 的度数为( )
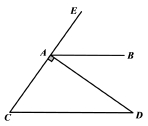
(A)25°
(B)35°
(C)45°
(D)55°
4.右图是某几何体的三视图,该几何体是
(A)三棱柱
(B)长方体
(C)圆锥
(D)圆柱
5.若正多边形的一个外角是 40°,则这个正多边形是
(A)正七边形
(C)正九边形
(B)正八边形
(D)正十边形
6.用配方法解一元二次方程 x - 6 x - 5 = 0 ,此方程可化为
(A)( x - 3)2= 4
(B)( x - 3)2= 14
(C)( x - 9)2= 4
(D)( x - 9)2= 14
7.如图,小明在地面上放了一个平面镜,选择合适的位置,刚好在平面镜中看到旗杆的顶部,此时小明与平面镜的水平距离为 2m,旗杆底部与平面镜的水平距离为 16m.若小明的眼睛与地面距离为 1.5m,则旗杆的高度为(单位:m)
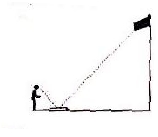
(A) (B)9 (C)12 (D)
8.某商店举行促销活动,其促销的方式是“消费超过 100 元时,所购买的商品按原价打 8折后,再减少 20 元” .若某商品的原价为 x 元(x>100),则购买该商品实际付款的金额(单位:元)是
(A) 80%x - 20 (B) 80% ( x - 20)
(C) 20%x - 20 (D) 20% ( x - 20)
9.某校合唱团有 30 名成员,下表是合唱团成员的年龄分布统计表:对于不同的 x,下列关于年龄的统计量不会发生改变的是
(A)平均数、中位数
(C)众数、中位数
(B)平均数、方差
(D)众数、方差
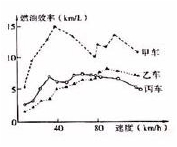
10.汽车的“燃油效率”是指汽车每消耗 1 升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗 1 升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗 1 升汽油行驶的里程数越少.右下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列说法中,
正确的是
(A)以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
(B)以低于 80km/h 的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少
(C)以高于 80km/h 的速度行驶时,行驶相同路程,丙车比乙车省油
(D)以 80km/h 的速度行驶时,行驶 100 公里,甲车消耗的汽油量约为 10 升
二、填空题(本题共 18 分,每小题 3 分)
11.分解因式:ax2 - 2ax+a=________.
12.若函数的图像经过点 A(1,2),点 B(2,1),写出一个符合条件的函数表达式_________.
13.下表记录了一名球员在罚球线上罚篮的结果:
这名球员投篮一次,投中的概率约是
14.如图,四边形 ABCD 是⊙O 内接四边形,若∠BAC=30°,∠CBD=80°,则∠BCD 的度
数为_________________.
第 14 题图
第 15 题
15.在平面直角坐标系 xOy 中,以原点 O 为旋转中心,将△AOB 顺时针旋转 90°得到
△A'OB',其中点 A'与点 A 对应,点 B'与点 B 对应.若点 A( - 3,0),B( - 1, 2),
则点 A'的坐标为_______________,点 B'的坐标为________________.
16.下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图 1,直线 l 和直线 l 外一点 P.
求作:直线 l 的平行直线,使它经过点 P.
作法:如图 2.
(1) 过点 P 作直线 m 与直线 l 交于点 O;
(2) 在直线 m 上取一点 A(OA
长为半径画弧,与直线 l 交于点 B;
(3) 以点 P 为圆心,OA 长为半径画弧,交直线 m 于点
C,以点 C 为圆心,AB 长为半径画弧,两弧交于点
所以直线 PD 就是所求作的平行线.
请回答:该作图的依据是
三、解答题(本题共 72 分,第 17-26 题,每小题 5 分,第 27 题 7 分,第 28 题 7 分,第 29
题 8 分)解答应写出文字说明、演算步骤或证明过程.
è 2 ø -1)0- 2sin60O + 3 - 2ïx + 72æ 1è y1 öx øx 2 - 2 xy + y 2x 2 y的值.
20. 如图,在△ABC 中,BC 的垂直平分线交 BC 于点 D,交 AB 延长线于点 E,连接 CE.
求证:∠BCE=∠A+∠ACB.
21.某科研小组计划对某一品种的西瓜采用两种种植技术种植.在选择种植技术时,该科研
小组主要关心的问题是:西瓜的产量和产量的稳定性,以及西瓜的优等品率. 为了解这两种
种植技术种出的西瓜的质量情况,科研小组在两块自然条件相同的试验田进行对比试验,并
从这两块实验田中各随机抽取 20 个西瓜,分别称重后,将称重的结果记录如下:
表 1
表 2
甲种种植技术种出的西瓜质量统计表
乙种种植技术种出的西瓜质量统计表
回答下列问题:
(1)若将质量为 4.5~5.5(单位:kg)的西瓜记为优等品,完成下表:
(2)根据以上数据,你认为该科研小组应选择哪种种植技术,并请说明理由.
22. 在平面直角坐标系 xOy,直线 y=x-1 与 y 轴交于点 A,与双曲线 y=kx交于点 B(m,2).
(1)求点 B 的坐标及 k 的值;
(2)将直线 AB 平移,使它与 x 轴交于点 C,与 y 轴交于点 D,若△ABC 的面积为 6,求直
线 CD 的表达式.
.如图,在23ABCD 中,对角线 BD 平分∠ABC,过点 A 作 AE//BD,交 CD 的延长线于点
E,过点 E 作 EF⊥BC,交 BC 延长线于点 F.
(1)求证:四边形 ABCD 是菱形;
(2)若∠ABC=45°,BC=2,求 EF 的长.
24. 汽车保有量是指一个地区拥有车辆的数量,一般是指在当地登记的车辆.进入 21 世纪
以来,我国汽车保有量逐年增长.下图是根据中国产业信息网上的有关数据整理的统计图.
2007—2015 年全国汽车保有量及增速统计图
根据以上信息,回答下列问题:
(1)2016 年汽车保有量净增 2200 万辆,为历史最高水平,2016 年汽车的保有量为万辆,与 2015 年相比,2016 年的增长率约为%;
(2)从 2008 年到 2015 年,
(3)预估 2020 年我国汽车保有量将达到
年全国汽车保有量增速最快;
万辆,预估理由是
25.如图,AB 为⊙O 的直径,C 为⊙O 上一点,过点 C 作⊙O 的切线,交 BA 的延长线交
于点 D,过点 B 作 BE⊥BA,交 DC 延长线于点 E,连接 OE,交⊙O 于点 F,交 BC 于点 H,
连接 AC.
(1)求证:∠ECB=∠EBC;
(2)连接 BF,CF,若 CF=6,sin∠FCB=求 AC 的长.
26.阅读下列材料:
某种型号的温控水箱的工作过程是:接通电源后,在初始温度 20℃ 下加热水箱中
的水;当水温达到设定温度 80℃ 时,加热停止;此后水箱中的水温开始逐渐下降,当
下降到 20℃ 时,再次自动加热水箱中的水至 80℃ 时,加热停止;当水箱中的水温下
降到 20℃ 时,再次自动加热,……,按照以上方式不断循环.
小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探
究.发现水温 y 是时间 x 的函数,其中 y(单位:℃ )表示水箱中水的温度.x(单位:min)
表示接通电源后的时间.
下面是小明的探究过程,请补充完整:
(1)下表记录了 32min 内 14 个时间点的温控水箱中水的温度 y 随时间 x 的变化情况
m 的值为
(2)①当 0≤x≤4 时,写出一个符合表中数据的函数解析式当 4
②如图,在平面直角坐标系 xOy 中,描出了上表中部分数据对应的点,根据描出的
点,画出当 0≤x≤32 时,温度 y 随时间 x 变化的函数图象:
(3) 如果水温 y 随时间 x 的变化规律不变,预测水温第 8 次达到 40℃时,距离接通电源 min.
27.在平面直角坐标系 xOy 中,二次函数 y=mx2 - (2m + 1)x + m - 5 的图象与 x 轴有两个公
共点.
(1)求 m 的取值范围;
(2)若 m 取满足条件的最小的整数,
①写出这个二次函数的解析式;
②当 n ≤ x ≤ 1 时,函数值 y 的取值范围是 - 6 ≤ y ≤ 4 - n,求 n 的值;
③将此二次函数平移,使平移后的图象经过原点 O.设平移后的图象对应的函数表达式为
y=a(x - h)2 + k,当 x < 2 时,y 随 x 的增大而减小,求 k 的取值范围.
.在28ABC 中,AB=BC,BD⊥AC 于点 D.
(1)如图 1,当∠ABC=90°时,若 CE 平分∠ACB,交 AB 于点 E,交 BD 于点 F.
①求证:△BEF 是等腰三角形;
②求证:BD=12(BC + BF);
(2)点 E 在 AB 边上,连接 CE.若 BD=12(BC + BE),在图 2 中补全图形,判断∠ACE 与
∠ABC 之间的数量关系,写出你的结论,并写出求解∠ACE 与∠ABC 关系的思路.
29.在平面直角坐标系 xOy 中,若点 P 和点 P1 关于 y 轴对称,点 P1 和点 P2 关于直线 l 对称,
则称点 P2 是点 P 关于 y 轴,直线 l 的二次对称点.
(1)如图 1,点 A(-1 , 0).
①若点 B 是点 A 关于 y 轴,直线 l1: x=2 的二次对称点,则点 B 的坐标为
②若点 C(-5 , 0)是点 A 关于 y 轴,直线 l2:x=a 的二次对称点,则 a 的值为
③若点 D( 2 , 1)是点 A 关于 y 轴,直线 l3 的二次对称点,则直线 l3 的表达式
为
(2)如图 2,⊙O 的半径为 1.若⊙O 上存在点 M,使得点 M'是点 M 关于 y 轴,直线 l4:x=b的二次对称点,且点 M'在射线 y =33x(x ³ 0) 上,b 的取值范围是
(3)E(t,0)是 x 轴上的动点,⊙E 的半径为 2,若⊙E 上存在点 N,使得点 N'是点 N关于 y 轴,直线 l5: y = 3x + 1的二次对称点,且点 N'在 y 轴上,求 t 的取值范围.
相关推荐:
各地2019中考报名时间 ※ 2019中考时间安排 ※ 关注微信先报名
2019中考报考指南 ※ 中考报名方法 ※ 中考报名条件
·2021年中考真题及答案解析专题 (2021-6-15 18:49:05)
·警方提醒:2021中考诈骗了解一下 千万注意! (2021-6-15 9:15:43)
·中考迎来“新调整” 2022年或将全面实行 (2021-5-25 17:26:34)
·好消息“体育”或将不被纳入中考 家长可以放心了 (2021-5-8 11:04:04)
·中考迎来大调整 550分以下考生或无缘高中! (2021-4-28 11:02:17)
2022年海南中考地理真题及答案已公布
2022年海南中考生物真题及答案已公布
2022年海南中考历史真题及答案已公布
2022年海南中考政治真题及答案已公布
2022年海南中考化学真题及答案已公布
2022年海南中考物理真题及答案已公布
2022年海南中考英语真题及答案已公布
2022年海南中考数学真题及答案已公布
2022年海南中考语文真题及答案已公布
| 国家 | 北京 | 天津 | 上海 | 重庆 |
| 河北 | 山西 | 辽宁 | 吉林 | 江苏 |
| 浙江 | 安徽 | 福建 | 江西 | 山东 |
| 河南 | 湖北 | 湖南 | 广东 | 广西 |
| 海南 | 四川 | 贵州 | 云南 | 西藏 |
| 陕西 | 甘肃 | 宁夏 | 青海 | 新疆 |
| 黑龙江 | 内蒙古 | 更多 | ||
·执业医师考试培训 试听 ·经济师考试培训 试听
·执业药师考试培训 试听 ·报关员考试培训 试听
·银行从业考试培训 试听 ·会计证考试培训 试听
·证券从业考试培训 试听 ·华图公务员培训 试听
·二级建造师考试培训 试听 ·公务员培训 网校 试听
·一级建造师考试培训 试听 ·结构师考试培训 试听
·注册建筑师考试培训 试听 ·造价师考试培训 试听
·质量资格考试培训 试听 ·咨询师考试培训 试听
·卫生职称考试培训 试听 ·监理师考试培训 试听





