 图1
图1
 图2
图2
 图3
图3
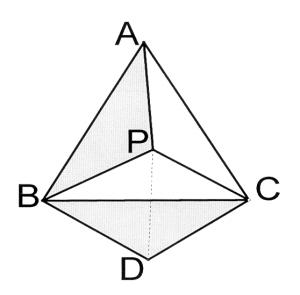 图4
图4
天津四中 马艳芳
精讲精练
随着新课程标准的实施,其基本理念对近几年中考数学命题的改革产生了重大影响。新课程标准下的初中数学教材,增添了图形变化的问题,使数学更贴近生活,几何变换这一重要的数学思想,在近几年的中考、竞赛试题中经常出现,这使得数学试题的解题方法和技巧更加灵活多变。只改变图形的位置,而不改变其形状大小,使几何图形重新组合,产生新的图形关系,从而找到解决问题的途径,这是进行几何变换的目的,其中旋转变换是最常见的手段之一。
旋转是几何变换中的基本变换,它一般先对给定的图形(或其中一部分图形),通过旋转,改变位置后重新组合,然后在新的图形中分析有关图形之间的关系,进而揭示条件与结论之间的内在联系,找出证题途径。
旋转变换是一种重要的几何变换,进行几何变换的目的有两个:
①揭示几何图形的性质或几何量之间的内在联系;
②使分散的元素集中,从而使表面互不相干的条件变得密切相关。
什么时候考虑用旋转变换?怎样运用旋转变换呢?下面结合例题谈谈旋转变换在平面几何解题中的应用:
例1.如图,正方形ABCD的边长为a,将正方形OMNP的一顶点O放在正方形ABCD的对角线AC、BD的交点处,你能求出两正方形重叠部分的面积吗?
这道题是初二课本上的一道课后练习题,当时我们解这道题时是从全等的角度来考虑的。现在我们可以尝试着用新方法——旋转来解这道题。
分析:重叠部分被分为两部分△OCF和△OCE,而△OCF ≌△OBE,△OCE≌△ODF,我们可以将△OCF绕点O顺时针旋转90°与原有的△OBE重合,或将△OCE绕点O逆时针旋转90°与原有的△ODF重合。这样,通过旋转我们能轻而易举地知道重叠部分面积为正方形ABCD面积的■,所以重叠部分面积为■a2。
解:∵OB=OC
∴将△OCF绕点O顺时针旋转90°
∴△OCF≌△OBE
∴S阴影=S△OBC
∴S阴影=■a2
这道题也可将△OEC绕点O逆时针旋转90°,进行解答。
这道题是通过旋转使图形与原有图形重合,从而使重叠部分面积得到重新组合,使问题得到解决。这个以前做过的题目,我们换一个角度再看这道题目,又别有一番风景。在感观上认识旋转,了解旋转解题的简便之处。从中总结出用旋转解题的前提条件——相交等线段,从感性认识上升到理性认识。
练习1.如右图所示,分别以正方形ABCD的边AB、AD为直径画半圆,若正方形的边长为a,求阴影部分的面积。
例2.如图所示,设P为等边△ABC内的一点,∠APB=113°,∠APC=123°
问:(1)PA、PB、PC能否构成三角形?
(2)如果能构成三角形,请找出构成的三角形各内角的度数。
分析:已知三条线段看它能否构成三角形,方法大概有两种。从计算的角度求三边长度,比较三边大小,利用三角形三边关系,判断能否构成三角形。或从图形的角度,看能否将其放入一个三角形中。根据本题的实际情况求三边长度不是很现实,所以问题的解决就是看能否把三条线段放入一个三角形中。如何将三条线段放入同一个三角形中?考虑到AB、BC为两条相交等线段——利用旋转,很好地解决了这一问题。
·2021中考语文阅读理解最全的33套答题公式 (2020-11-10 17:20:05)
·2020中考生物知识点结构图分类整理:健康的生活 (2019-11-8 14:54:53)
·2020中考生物知识点结构图分类整理:生物技术 (2019-11-8 14:53:20)
·2020中考生物知识点结构图分类整理:生物的多样性 (2019-11-8 14:50:27)
·2020中考生物知识点结构图分类整理:生物的生殖发育与遗 (2019-11-8 14:48:17)
2022年海南中考地理真题及答案已公布
2022年海南中考生物真题及答案已公布
2022年海南中考历史真题及答案已公布
2022年海南中考政治真题及答案已公布
2022年海南中考化学真题及答案已公布
2022年海南中考物理真题及答案已公布
2022年海南中考英语真题及答案已公布
2022年海南中考数学真题及答案已公布
2022年海南中考语文真题及答案已公布
| 国家 | 北京 | 天津 | 上海 | 重庆 |
| 河北 | 山西 | 辽宁 | 吉林 | 江苏 |
| 浙江 | 安徽 | 福建 | 江西 | 山东 |
| 河南 | 湖北 | 湖南 | 广东 | 广西 |
| 海南 | 四川 | 贵州 | 云南 | 西藏 |
| 陕西 | 甘肃 | 宁夏 | 青海 | 新疆 |
| 黑龙江 | 内蒙古 | 更多 | ||
·执业医师考试培训 试听 ·经济师考试培训 试听
·执业药师考试培训 试听 ·报关员考试培训 试听
·银行从业考试培训 试听 ·会计证考试培训 试听
·证券从业考试培训 试听 ·华图公务员培训 试听
·二级建造师考试培训 试听 ·公务员培训 网校 试听
·一级建造师考试培训 试听 ·结构师考试培训 试听
·注册建筑师考试培训 试听 ·造价师考试培训 试听
·质量资格考试培训 试听 ·咨询师考试培训 试听
·卫生职称考试培训 试听 ·监理师考试培训 试听

