2020江苏公务员考试行测备考：经典牛吃草问题

　　在公务员考试行测当中，数量关系对于大部分考生来说，是相对较难的一块。但即使这么难的数量关系，有一些题目依然可以套固定模型。牛吃草问题就是其中的一类题目。牛吃草问题只要出现了，就是很固定的一种模式。所以只要学好它，我们在考试中就一定能够拿下这类题型。那么今天，考试吧公务员考试网就来给大家讲讲怎么速解牛吃草问题!

　　一、牛吃草模型

　　【例1】牧场上有一片青草，每天都生长得一样快。这片青草供给10头牛吃，可以吃22天，或者供给16头牛吃，可以吃10天，期间一直有草生长。如果供给25头牛吃，可以吃多少天?这就是一道非常典型的牛吃草问题，典型的牛吃草问题的条件是设草的生长速度固定不变,不同头数的牛吃光同一片草地所需的天数各不相同,求若干头牛吃这片草地可以吃多少天。

　　二、解题技巧

　　牛吃草其实是是消长问题，如原来有一片草AB段。草继续保持原来的速度向右点生长，而牛开始吃草。在C点时，牛将新长出来的草和原来的草全都吃完了。将这个模型抽象成二维空间的图如下，我们可以发现，和我们学过的追及问题非常相似，因此类比追及问题来推导牛吃草问题的公式：

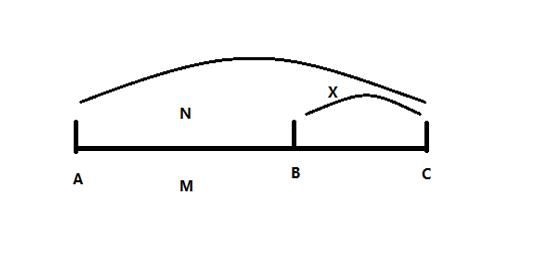
　　M：原来共有M份草。

　　N：有N头牛，每头牛每天吃1份草。牛吃草的速度为N份/天。

　　x：草每天生长x份草

　　t：牛把所有草吃光所花的时间

　　根据学过的追及问题的公式我们可以知道M=(N-x)·t。

　　所以根据公式，M=(10-x)×22=(16-x)×10。解得x=5，M=110。问25头牛可吃多少天则可列方程：M=(25-x)×t，带入可得t=5.5天

　　三、模型变形

　　1、相遇型

　　当寒冬来临，牛仔每天吃草的同时，草也在以一定的速度枯萎。此时，牛吃草问题又会变成什么样呢?

　　我们会发现牛吃的量与草枯死的量之和应该等于原有草量。这其实就是我们在行程问题当中的相遇问题。公式：M=(N+x)t。

　　【例2】寒冬已至，草场的草每天以一定的速度在枯死。如果有20头牛吃草，5天可以吃完，如果有15头牛吃草，6天可以吃完。假设每头牛每天吃的量时固定的，照此计算，想要10天把草吃完，需要多少头牛?

　　【参考答案】根据题目意思，枯死的草和牛所吃掉的草等于草场原有的草。

　　因此根据公式可得：M=(20+x)×5=(15+x)×6。解得x=10，M=150。想要在10天吃完则有M=(N+x)10。可得N=5。

　　1、极值型

　　我们一直在说合理放牧，说的是放牧的同时，不让草场的草被吃光。那么在这种情况下的牛吃草问题怎么去做呢?我们发现，只要牛吃草的速度追不上草生长的速度，草永远不会被吃光，此时最多可以养x头牛。因此在牛吃草问题中，若出现极值型的题目，一般考虑N=x的情况。

　　【例3】春天来了，草场的草又开始生长。如果有24头牛吃草，那么6天把草吃光，如果21头牛吃草，8天把草吃光。想要让草永远不被吃光，最多放几头牛吃草?

　　【参考答案】根据题目意思，草每天都在生长，当牛每天吃草的量等于草场每天生长的量，我们就能保证草能永远不被吃光。根据公式可得：M=(24-x)×6=(21-x)×8。解得x=12，M=72。即草每天都长5份，为了让草永远不被吃光，最多只能放5头牛吃草。

　　2、多个草场型

　　我们说一个草原上不可能只有一个草场，所以说又多出了一类问题，多个草场的牛吃草问题，是不同的牛数在不同的草场上的几种不同吃法，其中每头牛每天吃草量和草每天的生长量，两个量是不变的。我们可以通过最小公倍数法即通过寻找多个草场面积的“最小整数倍”，然后将所有面积都转化为“最小公倍数”，同时对牛的头数进行相应变化，然后进行解答。这样就变成了在相同面积草场的牛吃草问题，那么就可以直接使用牛吃草问题公式进行解答了。

　　【例4】20头牛，吃30公亩牧场的草15天可吃尽，15头牛吃同样牧场25公亩的草，30天可吃尽。请问几头牛吃同样牧场50公亩的草，12天可吃尽?

　　【参考答案】取30、25和50的公倍数300，所以原题等价于“300亩的牧场可供200头牛吃15天，可供180头牛吃30天，那么可供多少头牛吃12天”，300亩的草可供N头牛吃12天，那么有(200-x)×15=(180-x)×30=(N-x)×12，解得x=160，N=210，210÷6=35，所以35头牛吃同样牧场50公亩的草，12天可吃尽。

　　大家都学会怎么做牛吃草问题了吧。考试吧公务员考试网还会继续给大家解答行测中的各类问题，欢迎大家继续关注，同时祝各位考生成功上岸。

扫描/长按二维码可帮助公考通关

获取2020公考报名时间

获取2020年公考职位表

获取2020公考最新资讯

获取历年公考真题试卷

公务员万题库下载｜ 微信搜"万题库公务员考试"

　　相关推荐：

　　2020年公务员考试《行测》备考指导 |《申论》备考指导

　　历年公务员考试真题及答案汇总 | 2020年模拟试题汇总

　　2019公务员时事政治热点汇总 | 公务员考试经验 | 面试

　　2020公务员考试时间 | 2020公务员缴费时间 | 公考职位表