>>>2018年中级会计职称《财务管理》预习知识点汇总

　　货币时间价值的计算

　　(一)利息的两种计算方法

　　单利计息：只对本金计算利息，各期利息相等。

　　复利计息：既对本金计算利息，也对前期的利息计算利息，各期利息不同。

　　(二)复利终值与现值的计算

　　终值(Future Value)是现在的一笔钱或一系列支付款项按给定的利息率计算所得到的在某个未来时间点的价值。

　　现值(Present Value)是未来的一笔钱或一系列支付款项按给定的利息率计算所得到的现在的价值。

　　【教材例2-1】某人将100元存入银行，复利年利率2%，求5年后的终值。

　　复利终值的计算公式

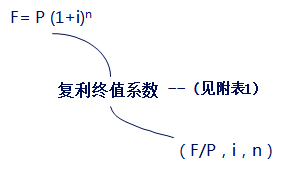
　　复利终值系数表

　　1元的复利终值系数，利率I,期数 n 即(F/P,i,n)。

　　【教材例2-1解答】

　　F=P(1+i)n

　　=100×(l+2%)5=110.41 (元)

　　或：

　　F=P×(F/P,i,n)

　　=100×(F/P,2%,5)

　　=100×1.1041=110.41 (元)

　　2、复利现值

　　复利现值计算公式：

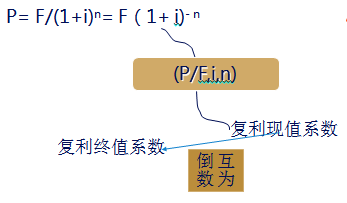
　　【教材例2-2】某人为了5年后能从银行取出100元，在复利年利率2%的情况下，求当前应存入金额。

　　复利现值系数表

　　期数为n的复利现值系数(P/F,i,n )

　　【解答】

　　P=F/(1 +i)n

　　=100/(1 +2% )5=90. 57 (元)

　　或：

　　P=F×(P/F,i,n)

　　=100×(P/F,2%,5)

　　=100×0.9057=90.57

　　【例题·计算题】某人拟购房，开发商提出两种方案，一是现在一次性付80万元，另一方案是5年后付100万元若目前的银行存款利率是7%，应如何付款?

　　复利终值系数表

　　1元的复利终值系数，利率I,期数 n 即(F/P,i,n).

　　复利现值系数表

　　期数为n的复利现值系数( P/F,i,n )

　　【例题答案】

　　(1)用终值比较：

　　方案一的终值：F =800000×(1+7%)5=1122080

　　或 F =800000 ×(F/P，7%，5)=800000×1.4026=1122080

　　方案二的终值：F=1000000

　　所以应选择方案二。

　　(2)用现值比较

　　方案二的现值：P = 1000000×(1+ 7%)-5

　　或P=1000000×(P/F，7%,5 )=1000000×(0.713)

　　=713000<800000

　　解答：按现值比较，仍是方案2较好

　　结论：

　　(1)复利的终值和现值互为逆运算。

　　(2)复利的终值系数(1+i)n和复利的现值系数1/(1+i)n互为倒数。

扫描/长按二维码帮助会计师考试通关

2017中级会计成绩查询

2018初级会计报名时间

下载历年会计师真题卷

了解2018会计报考指南

会计职称万题库下载 | 微信搜索"万题库会计职称考试"

　　相关推荐：

　　2018年中级会计师考试应该何时开始复习

　　各地2017年中级会计职称成绩查询时间汇总

　　考试吧中级会计职称考试各科目每日一练汇总

　　2018年中级会计职称各阶段考试真复习计划汇总